Métricas de avaliação para clusterização
10 minutos de leitura
Autor(a)
allan-spadini
Inscreva-se em nossa Newsletter
Fique por dentro de conteúdos, insights e oportunidades do universo tech. Receba novidades e lançamentos direto no seu e-mail.
10 minutos de leitura
Autor(a)
Fique por dentro de conteúdos, insights e oportunidades do universo tech. Receba novidades e lançamentos direto no seu e-mail.
Imagine que você trabalha como Cientista de Dados em uma empresa de varejo online e se deparou com um desafio: um vasto dataset contendo milhões de interações de clientes, abrangendo compras, navegação e feedback.
Sem informações prévias sobre o conjunto de dados, seu objetivo se tornou descobrir padrões ocultos que pudessem ser relevantes para a estratégia de marketing e otimização de produtos.
Você percebeu que o clustering seria uma solução promissora para esse problema. O clustering (ou agrupamento) é uma técnica de aprendizado de máquina não supervisionada que nos permite segmentar dados em grupos (ou clusters) com características semelhantes.
Se você deseja saber mais sobre os tipos de aprendizagem de máquina, vai gostar de conhecer o artigo Quais são os 4 tipos de aprendizagem na IA, algoritmos e usos no dia a dia.
Porém, há uma variedade de técnicas de clustering disponíveis, como o K-means, clustering hierárquico e DBSCAN.
Então, alguns questionamentos podem surgir, como você pode avaliar a eficácia dos diferentes métodos de clustering e assegurar que as segmentações de clientes sejam, de fato, significativas e úteis?
Neste artigo, vamos explorar algumas das métricas para a avaliação de clustering, como o índice Davies-Bouldin, o Silhouette Score e o índice Dunn, e discutiremos como aplicá-las efetivamente para extrair insights valiosos de seus datasets.
Neste processo, você tem a possibilidade de analisar as métricas de avaliação para clusterização de forma contextualizada, a fim de observar como assumem um papel importante.
Elas nos fornecem um meio quantitativo para avaliar e comparar a qualidade dos clusters criados, nos orientando na escolha da técnica mais adequada para nosso contexto específico. Então, vamos lá!
Imagine que você aplicou um método de clustering sobre o seu dataset com objetivo de segmentar e obteve um resultado.
Avalie este artigo
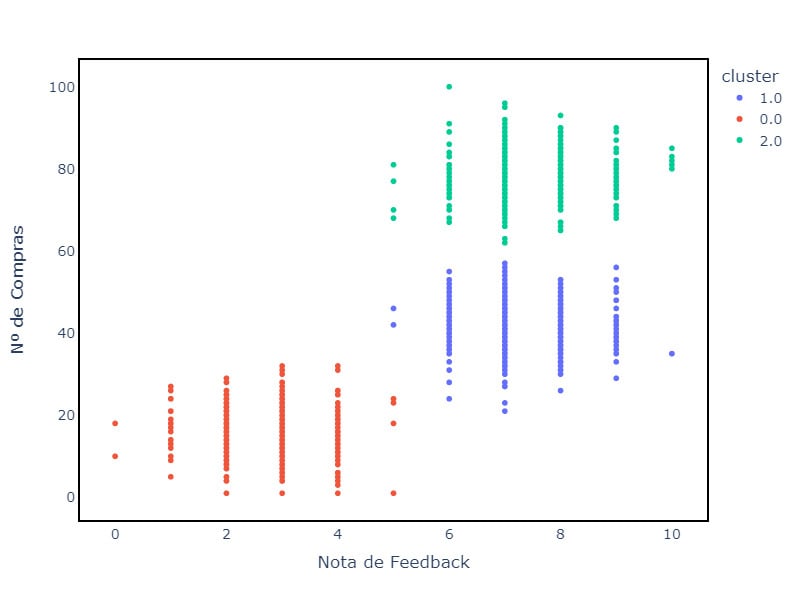
No gráfico abaixo temos um exemplo que ilustra o resultado de aplicar um método de clustering ao seu conjunto de dados.
Cada ponto representa uma observação, colorida de acordo com o cluster atribuído. A disposição dos pontos nos oferece pistas visuais sobre a coesão e separação entre os grupos.
No entanto, surge uma questão: será que o número de clusters escolhido reflete a estrutura natural dos dados? Este é o momento de aplicar métricas de avaliação de clustering.
Nesse contexto, a coesão e separação são métricas cruciais para avaliar a qualidade dos clusters formados por algoritmos de agrupamento.
Eles ajudam a entender o quão bem o algoritmo está performando em termos de agrupar dados similares e separar dados distintos.
A coesão se refere à proximidade dos pontos de dados dentro do mesmo cluster. Quanto menor a distância entre os pontos dentro de um cluster, maior a coesão. Isso indica que os membros do cluster são similares entre si.
Em outras palavras, um cluster possui alta coesão quando os dados dentro dele estão bem compactados e próximos ao centro do cluster (centróide).
Geralmente, a coesão é medida pela soma das distâncias de cada ponto de dados até o centróide do seu respectivo cluster.
O termo separação, por outro lado, se refere ao quão distintos ou separados estão os clusters uns dos outros.
Um bom agrupamento deve ter uma alta separação, significando que os clusters não estão se sobrepondo e são bem distintos entre si.
Em essência, a separação avalia o quão bem os clusters estão isolados um do outro. Essa medida pode ser obtida calculando-se a distância entre os centróides de diferentes clusters.
Quanto maior essa distância, maior a separação. Outra possibilidade é considerar a distância mínima entre pontos de clusters diferentes para medir a separação.
Combinando a coesão e separação, teremos uma visão robusta da qualidade da clusterização. Idealmente, você quer clusters altamente coesos e bem separados.
Essas métricas ajudam a otimizar parâmetros de algoritmos de clustering, como o número de clusters no método K-means, por exemplo.
É na aplicação do K-Means que normalmente essas métricas fazem sentido. Com a sklearn, podemos medir a coesão a partir do método inertia_, como mostrado no exemplo:
from sklearn.cluster import KMeans
# Supondo que você tenha um conjunto de dados X
# Ajustar o modelo K-Means
kmeans = KMeans(n_clusters=3, random_state=42).fit(X)
# A coesão pode ser acessada através de inertia_
coesao = kmeans.inertia_
print("A coesão (WCSS) dos clusters é:", coesao)
No caso da separação não existe um método específico, mas podemos calcular seu valor manualmente:
# Calcular o centroide global
centroide_global = np.mean(X, axis=0)
# Calcular a separação
separacao = np.sum([np.linalg.norm(centroide - centroide_global) ** 2 for centroide in kmeans.cluster_centers_])
print("A separação dos clusters é:", separacao)
O Silhouette Score também é uma métrica bastante usada para avaliar a clusterização. Porém, o Silhouette Score fornece uma medida compreensiva que leva em conta tanto a coesão quanto a separação dos clusters.
Chamando a coesão de a e separação de b o Silhouette Score para um único ponto é obtido pela fórmula s = (b-a)/(max(a,b)) .
O valor dessa métrica varia de menos um a um. Valores próximos de um indicam que o ponto está bem ajustado ao seu próprio cluster e mal ajustado aos clusters vizinhos. Se o valor é próximo de zero, temos um ponto que está próximo a um limite de decisão entre dois clusters.
Já um valor negativo indica que o ponto pode ter sido atribuído ao cluster errado. Além disso, podemos calcular o Silhouette score para todo o conjunto de pontos. A Sklearn possui essa métrica implementada.
from sklearn.metrics import silhouette_score
# Aplicando o K-means para clusterizar os dados
kmeans = KMeans(n_clusters=3, random_state=0).fit(X)
labels = kmeans.labels_
# Calculando o Silhouette Score
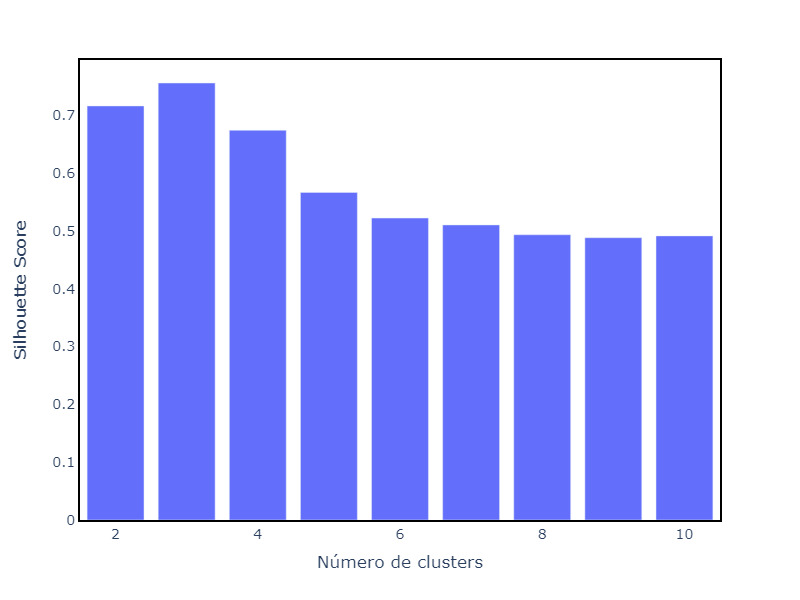
score = silhouette_score(X, labels)
O Silhouette Score é bastante usado para avaliar se o número de clusters escolhido é adequado. Nesse caso, é útil visualizar como o valor da métrica muda com o número de clusters.
No exemplo, plotamos barras indicando o valor do Silhouette Score para diferentes números de clusters. Repare que o valor quando usamos 3 clusters é maior do que para as outras tentativas.
Esse método, quando aplicado a clusterização, também tem o objetivo de identificar o número ideal de clusters. Nesse caso, identificamos o ponto em que a inclusão de clusters adicionais resulta em ganhos marginais na explicação da variância total nos dados.
Isto é, busca-se o número de clusters onde a adição de mais grupos apenas contribui minimamente para a explicação da variância observada. A coesão é a métrica que pode ser usada para medir a variância dos grupos.
Calculando os valores de coesão para um número de clusters específico dividido pela soma do valor de coesão de todos os clusters testados temos a Porcentagem da Variância Explicada, como se pode observar na imagem a seguir.
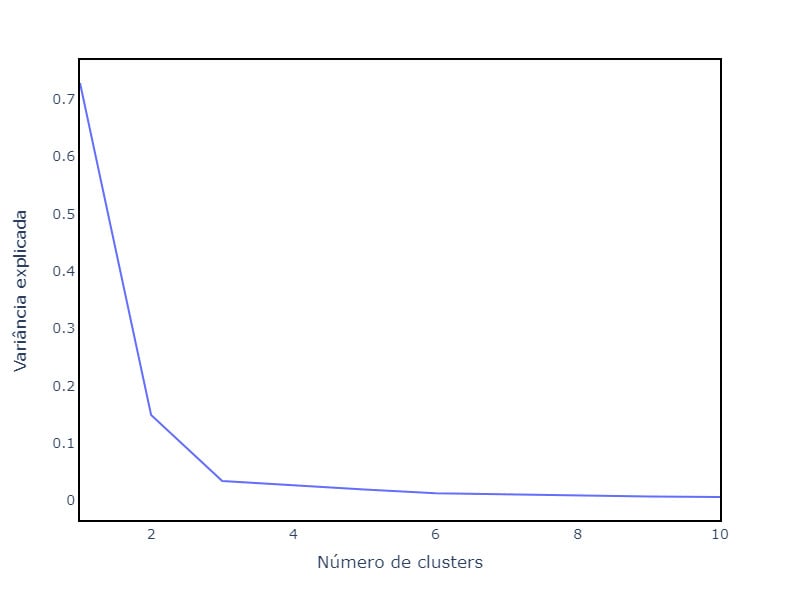
Nesse caso, o ponto no gráfico onde o aumento do número de clusters deixa de representar um ganho substancial na variância é o número de três clusters, o “cotovelo” do gráfico.
Dentre as métricas estudadas, podemos ressaltar algumas vantagens e limitações de cada uma.
| Métrica | Vantagens | Limitações |
|---|---|---|
| Coesão | Simplicidade no entendimento e cálculo; fornece uma medida direta da compactação interna dos clusters. | Não considera a separação entre clusters; pode ser enganosa se usada isoladamente, pois um modelo pode ter uma boa coesão mas uma separação ruim. |
| Separação | Ajuda a entender a distinção entre clusters; uma métrica importante para evitar a mistura de diferentes grupos. | Não considera a coesão interna dos clusters; um alto valor de separação não garante que os pontos dentro de um cluster sejam similares entre si. |
| Silhouette Score | Fornece uma visão balanceada que considera tanto a coesão quanto a separação; útil para comparar a qualidade de diferentes clusterizações. | Pode ser computacionalmente custoso para grandes conjuntos de dados. |
Quando falamos de métricas é comum levar em consideração o método K-Means, já que elas são úteis para determinar o número ideal de clusters.
Essa é uma incógnita na aplicação do K-Means. Porém, métodos como o Silhouette Score são aplicáveis em conjunto com qualquer método de clusterização com a finalidade de verificar a qualidade da clusterização.
Outros métodos que podem ser citados são os índices de Davies-Bouldin, de Dunn e de Calinski-Harabasz.
Esses índices são semelhantes às métricas anteriores, tentam avaliar elementos como a separação, dispersão e densidade de clusters.
Outra possibilidade é a utilização de medidas de validade externas. Essas são utilizadas para avaliar a qualidade de uma solução de clusterização quando o verdadeiro agrupamento dos dados é conhecido.
Essas medidas comparam a clusterização obtida com a classificação real, oferecendo uma perspectiva sobre quão bem o modelo de clusterização capturou a estrutura inerente dos dados conforme definido por algum critério externo.
Alguns exemplos de métricas de validade externas são:
Por fim, podemos utilizar métodos baseados em estabilidade. Esses avaliam a estabilidade dos clusters gerados pela repetição do método de clusterização em subconjuntos de dados ou dados perturbados e observando a consistência dos clusters resultantes.
Esses métodos são úteis para verificar a robustez dos clusters identificados, ajudando a determinar se as formações dos grupos são genuínas ou produto de variabilidade aleatória nos dados.
Ao medir a estabilidade, é possível ter uma noção da confiabilidade dos clusters gerados e da escolha do número de clusters.
A escolha e aplicação de métricas de avaliação em clusterização são cruciais para assegurar a qualidade e a relevância dos clusters identificados.
Neste artigo, tivemos a possibilidade de explorar sobre as métricas essenciais, como coesão, separação e Silhouette Score, ressaltando sua importância para entender a compactação e distinção dos clusters.
Adicionalmente, destacamos os métodos de estabilidade, enfatizando a importância de validar a consistência dos clusters em diferentes condições. Abordagens como essa garantem que as decisões tomadas com base na clusterização sejam informadas e confiáveis, fortalecendo as estratégias de análise de dados.
Cada métrica tem suas particularidades e pode ser mais adequada para certos tipos de dados ou objetivos de clusterização.
Ao escolher uma métrica, é crucial considerar a natureza do método de clusterização e a estrutura intrínseca dos dados.
Power BI ou Excel: qual a melhor opção para Business Intelligence?
Ler mais
SQL: como usar as cláusulas UPDATE e DELETE para atualizar e deletar dados em tabelas
Ler mais
Analista de BI em T: o que faz, competências e habilidades
Ler mais