PCA em Python: Visualizando dados em 5d?
Se eu tenho informações em 5 dimensões, eu consigo ver elas em 2d? Para responder essa pergunta, gosto da analogia da viagem. Se você foi para Tokyo e Paris, gostou muito das duas cidades e quando volta para o Brasil gostaria de compará-las. Você consegue ver Tokyo e Paris ao mesmo tempo, no Brasil?
Claro! É só olhar as fotos que tirou nas duas cidades. E para vê-las ao mesmo tempo, basta colocar as duas fotos lado a lado.
Mas aí você diz: Guilherme, você roubou, pois a foto diminuiu a experiência 3d da viagem em duas imagens 2d, perdendo informações. Claro, mas mesmo diminuindo em uma dimensão e perdendo informações, as fotos conseguem passar a mensagem que eu desejava visualizar: comparar as duas cidades/viagens - na verdade perdemos também a quarta dimensão, o tempo que passou durante a viagem.

Essa ideia de diminuir a dimensão de um conjunto de dados para poder visualizá-los em 2d (3d etc) pode ser alcançada no mundo dos dados através da análise deles. Um método estatístico para diminuir dimensões é o PCA, podendo ser usado não só para visualização, mas em outras situações importantes de análise também.
Para usar o PCA existem diversas características importantes (como a escala dos dados nas diversas dimensões) portanto vamos ver um exemplo baseado em algo do mundo real?
Opa, mas que dado do mundo real tem mais de 2 ou 3 dimensões? Vamos pensar nos cursos que um aluno faz na Alura, seguindo o post e o código anterior sobre o assunto, eu sou capaz de gerar matrículas aleatórias em N cursos:
def matriculas_aleatorias(n):
return (np.random.randn(ALUNOS, n) + 3).astype(int)
E gerar alunos que tenham mais matrículas numa categoria de cursos do que em outras categorias:
def gera_alunos(categorias, categoria):
linhas = matriculas_aleatorias(len(categorias))
alunos = pd.DataFrame(linhas, columns=categorias)
alunos[categoria] = muitos_cursos()
alunos['categoria'] = categoria
return alunos
E podemos gerar todos os alunos, de todas as categorias de uma vez só:
def gera_todos_os_alunos(categorias):
alunos = pd.DataFrame([], columns = categorias)
for categoria in categorias:
novos = gera_alunos(categorias, categoria)
alunos = alunos.append(novos, sort=False)
return alunos
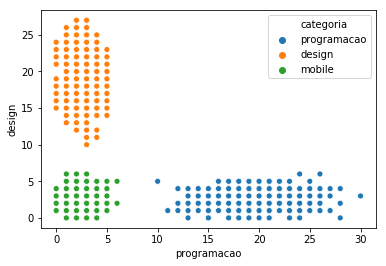
Pronto, o código que me interessa é o que gera alunos que fazem cursos em 3 categorias. Teremos um grupo de alunos e alunas que faz mais programação, outro design, outro mobile. E plotamos como no post anterior:
alunos = gera_todos_os_alunos(['programacao', 'design', 'mobile'])
sns.scatterplot(x="programacao", y="design", hue="categoria", data=alunos)

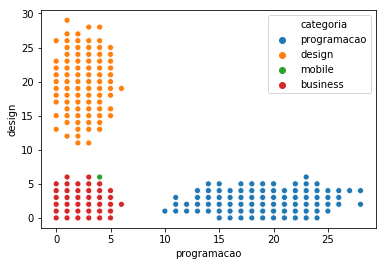
E podemos facilmente gerar agora 4 categorias.
alunos = gera_todos_os_alunos(['programacao', 'design', 'mobile', 'business'])
sns.scatterplot(x="programacao", y="design", hue="categoria", data=alunos)
Repare que um aluno que faz 3, 4, 2 e 15 cursos agora é (3, 4, 2, 15) e no plano em R^2 está aparecendo em (3,4)... juntamente com uma aluna que fez 3, 4, 15, 2 cursos. Que horror, visualmente ao descartar duas das quatro dimensões, perdemos muitas informações (óbvio):
Podemos ser mais maldosos e tentar analisar os alunos em 5 dimensões:
alunos = gera_todos_os_alunos(['programacao', 'design', 'mobile', 'business', 'frontend'])
sns.scatterplot(x="programacao", y="design", hue="categoria", data=alunos)
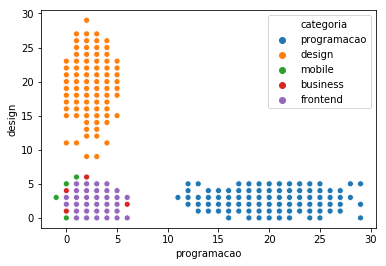
Como vimos, reduzir a dimensão simplesmente apagando elas é uma perda de informação que visualmente não nos diz o que queremos ver. Outra maneira é usar uma técnica já estabelecida que tenta mapear no 2d (ou Nd) um número maior de dimensões, vamos mapear em 2 dimensões nossos alunos e alunas, e plotá-los:
from sklearn.decomposition import PCA
alunos_sem_categoria = alunos.drop("categoria", axis=1)
pca = PCA(n_components=2)
pca.fit(alunos_sem_categoria)
r2 = pca.transform(alunos_sem_categoria)
plt.scatter(r2[:,0], r2[:,1])

Como fizemos anteriormente, podemos pintar de acordo com a categoria de curso mais feito:
cores = {'programacao':1, 'mobile':2, 'design':3, 'business':4, 'frontend':5}
plt.scatter(r2[:,0], r2[:,1], c=alunos.categoria.apply(lambda x: cores[x]), cmap='tab10')

Por fim, uma última refatoração para não precisar toda vez definir a variável cores:
def cores_para_categorias(valores):
cores = {key: index for index, key in enumerate(valores.unique())}
return valores.apply(lambda x: cores[x])
plt.scatter(r2[:,0], r2[:,1], c=cores_para_categorias(alunos.categoria), cmap='tab10')
Com o mesmo resultado visual:

Um ponto importante é que o PCA tende a dar mais peso para dimensões (pode pensar intuitivamente em eixos) com valores mais extremos, por isso seria interessante que todas as dimensões possuissem valores bem distribuídos. No nosso exemplo eles já tem valores máximos, mínimos e de distribuição próximas pois usamos distribuições normais para gerar nossos dados.
Mas e se os dados estivessem em escalas distintas? Podemos "normalizar" os dados, e existem diversas maneiras de reescalar informações. Uma delas é diminuir todos os pontos pela média e dividir pelo desvio padrão. Isso faz com que todos os dados transformados estejam entre -1 e 1 - todos numa mesma escala. Em Python podemos fazer isso usando um StandardScaler e colocando junto com o PCA:
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
pca = make_pipeline(StandardScaler(), PCA(n_components=2))
pca.fit(alunos_sem_categoria)
r2 = pca.transform(alunos_sem_categoria)
plt.scatter(r2[:,0], r2[:,1], c=cores_para_categorias(alunos.categoria), cmap='tab10')
O resultado é diferente mas a dimensão continua sendo 2 e temos a visualização e informações que buscávamos:

Por fim, com um pouco mais de código podemos extrair os coeficientes de redução de dimensão do PCA (coeff) e utilizá-los para mostrar como as 5 dimensões foram mapeadas em R^2:
pca = PCA(n_components=2)
pipe = make_pipeline(StandardScaler(), pca)
pipe.fit(alunos_sem_categoria)
r2 = pipe.transform(alunos_sem_categoria)
plt.scatter(r2[:,0], r2[:,1], c=cores_para_categorias(alunos.categoria), cmap='tab10')
coeff = np.transpose(pca.components_)
for i in range(5):
plt.arrow(0, 0, coeff[i,0], coeff[i,1],color = 'red',alpha = 0.5)
plt.text(coeff[i,0]* 1.5, coeff[i,1] * 1.5, alunos.columns[i], color = 'red', ha = 'center', va = 'center')
plt.xlim(-3,3)
plt.ylim(-3,3)Por causa da natureza do PCA, como os eixos originais (direção) e suas influências (tamanho) são plotados indicam para onde eles foram parar no novo mapa (nosso plot). Quanto maior a correlação entre duas dimensões originais, mais dois eixos estariam alinhados.
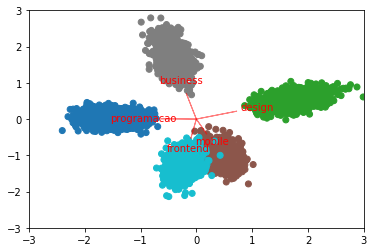
Claro, ao reduzirmos o número de dimensões - mesmo em um exemplo didático - perdems informação. Seja na visualização ou para o processamento dos dados PCA é um recurso que oferece uma troca: uma certa perda de informação para podermos executar algoritmos em dimensões menores (uso preparatório) ou analisarmos os dados visualmente (uso exploratório).
Note que o objetivo dos posts não foi detectar agrupamentos (clustering), mas com certeza é mais fácil visualizar clusters num plot 2d do que num plot 5d (há!) até mesmo depois do processamento. Claro, se você é sortudo ou sortuda, e seus dados iniciais já eram em duas dimensões, maravilhas, mas se como no mundo real, o número de features e dimensões é bem maior, recorremos a métodos de redução de dimensão para analisar nossos dados.
Você pode encontrar todo o código da plotagem em 2d, 3d e PCA no github. Dentre alguns dos cursos existentes de Data Science e Machine Learning na Alura, PCA pode ser utilizado no preparo e visualização dos dados, além da diminuição de dimensões e escolha de features.