Redes neurais: o que são e como funcionam

As redes neurais revolucionaram o campo da inteligência artificial e do Machine Learning, permitindo avanços significativos em áreas como reconhecimento de voz, processamento de imagens, tradução automática e até mesmo diagnósticos médicos.
Mas o que torna as redes neurais tão poderosas? E como elas funcionam por trás das cortinas?
Para responder a essas questões, o objetivo desse artigo é refletir sobre o que são as redes neurais, como funcionam e como podem ser aplicadas em diversos contextos — desde a previsão de vendas até a classificação de imagens médicas.
O que são redes neurais?
Imagine poder construir modelos que aprendem e se adaptam a partir de dados complexos, capturando padrões sutis que escapam às técnicas tradicionais. É exatamente isso que as redes neurais fazem.
Elas são inspiradas na estrutura do cérebro humano e têm a capacidade de resolver problemas altamente não lineares, tornando-se uma ferramenta essencial para cientistas de dados e engenheiros.

Cenário prático: como aplicar as redes neurais para prever vendas
Você trabalha como cientista de dados em uma empresa de varejo e recebeu a tarefa de desenvolver um modelo para prever as vendas de um determinado produto nos próximos meses.
Seu chefe enfatizou que este é um problema altamente não linear, influenciado por diversos fatores, e mencionou que já havia obtido sucesso utilizando redes neurais. Mas o que exatamente são redes neurais e como elas podem ajudar?
Ao pesquisar, você nota que a biblioteca Scikit-learn oferece métodos para redes neurais e que existem outras bibliotecas populares como TensorFlow, Keras e PyTorch.
No entanto, tudo parece bem diferente dos métodos clássicos de machine learning com os quais você está mais familiarizado. Então surge o questionamento: por onde começar? E qual dessas ferramentas escolher para dar o primeiro passo?
Se você quer entender ainda mais sobre como as redes neurais estão transformando a inteligência artificial, vale a pena conferir o vídeo abaixo. Ele explica de forma didática como essas tecnologias funcionam na prática.
A estrutura de uma rede neural
Retomando o problema, temos uma tabela que contém informações relacionadas às vendas de um produto. As primeiras colunas da tabela correspondem a fatores que influenciam as vendas, enquanto a última coluna representa a quantidade de produtos vendidos.
| Mes | Estoque | Precipitacao | Dias_Promocao | Vendas |
|---|---|---|---|---|
| 7 | 111 | 21.3961 | 2 | 49.0838 |
| 4 | 3 | 152.206 | 3 | 0.0000 |
| 11 | 349 | 108.253 | 9 | 115.254 |
| 8 | 330 | 192.598 | 8 | 96.4274 |
| 5 | 445 | 68.3744 | 5 | 85.4793 |
| ... | ... | ... | ... | ... |
| 6 | 429 | 97.4312 | 1 | 106.739 |
| 11 | 269 | 165.897 | 0 | 101.186 |
| 2 | 485 | 57.7175 | 5 | 91.7283 |
| 11 | 470 | 116.109 | 7 | 126.533 |
| 3 | 324 | 132.022 | 6 | 75.7136 |
Nosso objetivo é construir um modelo que receba as informações sobre Mês, Estoque, Precipitação e Dias de Promoção, sendo capaz de prever a quantidade de vendas de um produto.
Para atingir esse objetivo, utilizaremos uma rede neural, que pode ser entendida como um conjunto de "neurônios" artificiais organizados em camadas.
Esses neurônios processam informações e fazem previsões, permitindo que a rede capture padrões complexos nos dados.
A rede que vamos utilizar pode ser visualizada na figura abaixo:
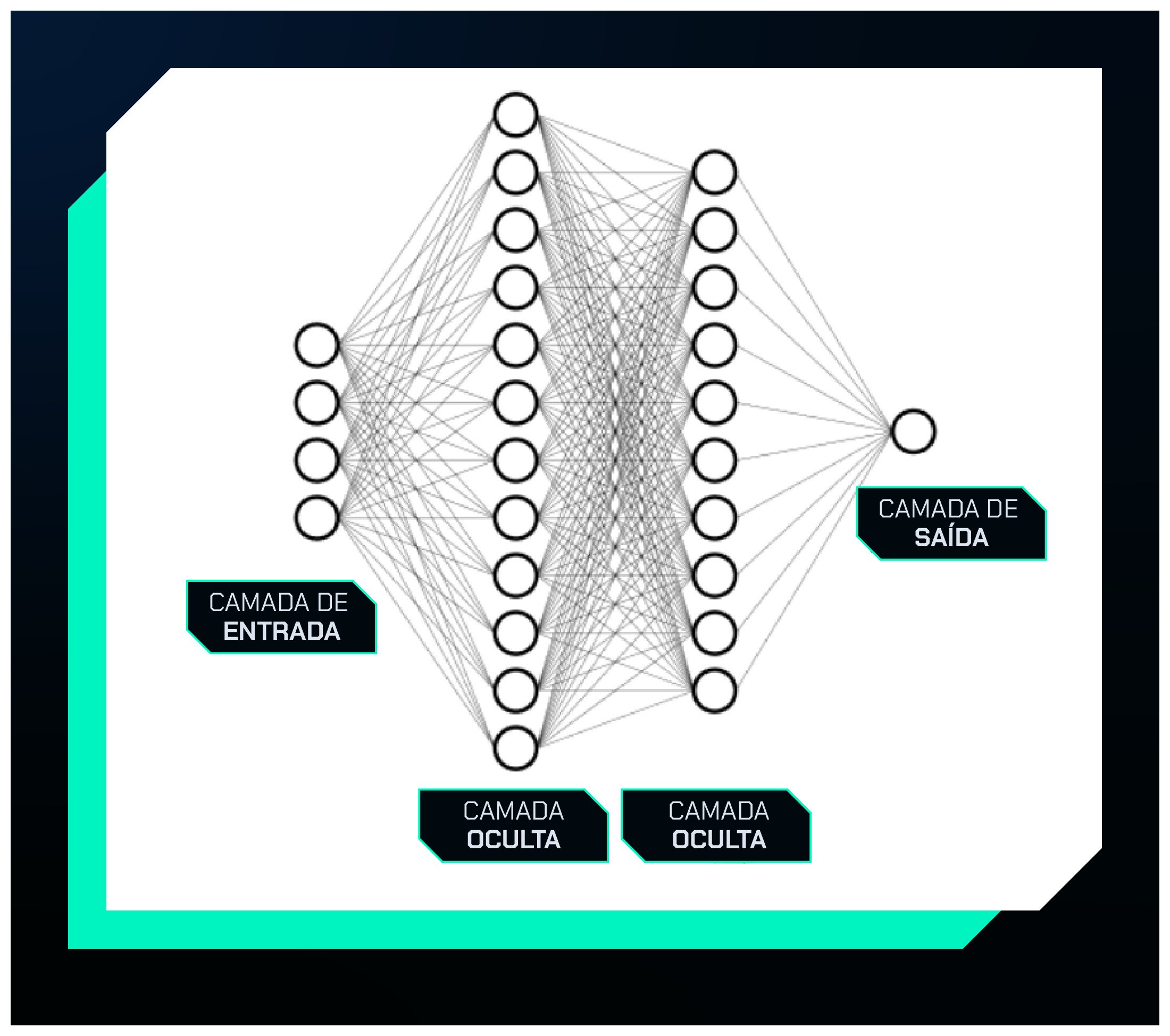
Na figura, vemos uma camada de entrada com quatro entradas que representam o Mês, Estoque, Precipitação e Dias de Promoção.
Em seguida, temos duas camadas ocultas (hidden layers), onde cada círculo (neurônio) recebe informações da camada anterior. Esses neurônios aplicam uma soma ponderada das entradas e utilizam uma função de ativação para gerar suas saídas, passadas para a próxima camada.
Esse processo continua até atingirmos a camada de saída, que, no nosso caso, possui apenas um neurônio.
Esse neurônio final será responsável por gerar a previsão da quantidade de produtos vendidos, após passar pela sua própria função de ativação.
Quer aprofundar ainda mais seu conhecimento sobre deep learning? O vídeo a seguir oferece uma explicação clara e direta sobre como essa tecnologia funciona e por que ela é tão poderosa.
Agora, você pode estar se perguntando: Como funcionam essas somas ponderadas? O que são essas funções de ativação?
Vamos explorar mais a fundo os conceitos de somas ponderadas e funções de ativação, elementos cruciais para o funcionamento dessas redes.
Entendendo pesos e bias nas redes neurais
Ainda na imagem da rede neural, cada valor da entrada é ligado por uma reta a cada neurônio da camada seguinte. A cada uma dessas ligações atribuímos um peso, um valor que será multiplicado pela entrada.
Esse peso serve para expressar a importância que uma determinada ligação na rede vai ter na estrutura da rede como um todo.
De forma mais detalhada, um neurônio recebe várias entradas, que podem ser variáveis de um conjunto de dados ou saídas de outros neurônios em camadas anteriores. Cada uma dessas entradas (x1,x2,...,xn) é multiplicada por um peso (w1,w2,...,wn) que define a importância de cada entrada para o neurônio.
As entradas multiplicadas pelos seus respectivos pesos são somadas. Esse somatório ponderado é essencialmente uma combinação linear das entradas. Matematicamente, é expresso como:
z=w1x1+w2x2+...+wnxn+b
Aqui:
- xi são as entradas,
- wi são os pesos,
- b é o bias, que ajusta o resultado, garantindo que o neurônio tenha flexibilidade mesmo com entradas iguais a zero.
Função de ativação
Após calcular a soma ponderada (zzz), o neurônio aplica uma função de ativação. A função de ativação introduz não linearidade no modelo, permitindo que a rede neural capture padrões complexos nos dados.
As funções de ativação mais comuns são:
- ReLU (Rectified Linear Unit): Retorna zero para valores negativos e retorna o valor original para valores positivos.
- Sigmoide: Converte o valor z em uma probabilidade entre 0 e 1.
- Tangente hiperbólica (Tanh): Transforma o valor z em um intervalo entre -1 e 1.
No nosso problema, estamos lidando com a previsão de vendas, que é um valor contínuo e não negativo.
Portanto, uma função de ativação como ReLU pode ser adequada para a camada de saída.
O processo de treinamento
Ao definir a estrutura da rede neural, ainda não sabemos quais são os pesos e bias corretos que permitem que a rede faça previsões precisas. É
aqui que entra o processo de treinamento, no qual a rede aprende a ajustar esses parâmetros com base nos dados de treinamento.
Propagação (Forward Propagation)
Inicialmente, os pesos são definidos aleatoriamente. Durante a propagação para frente, as entradas são passadas através da rede, camada por camada, até chegar à saída final.
Em cada neurônio, é calculada a soma ponderada das entradas e aplicada a função de ativação.
Cálculo do Erro
A saída gerada pela rede é então comparada com o valor real das vendas. A diferença entre a previsão e o valor real é o erro (ou perda), que precisamos minimizar.
Retropropagação (Backpropagation) e Gradiente Descendente
Para ajustar os pesos e minimizar o erro, utilizamos o algoritmo de retropropagação combinado com o gradiente descendente.
- Gradiente Descendente: É um método de otimização que ajusta os pesos na direção oposta ao gradiente do erro em relação aos pesos. Isso significa que estamos movendo os pesos na direção que mais reduz o erro.
- Retropropagação: É o processo pelo qual calculamos o gradiente do erro em relação aos pesos, começando pela camada de saída e retrocedendo até a camada de entrada. Essa informação é usada para atualizar os pesos de cada conexão.
Esse ciclo de propagação para frente, cálculo do erro, retropropagação e atualização dos pesos é repetido muitas vezes (épocas) até que o erro seja minimizado e a rede aprenda a fazer previsões precisas.
Qual é a relação entre redes neurais e regressão linear?
De fato, há uma relação. A regressão linear é um modelo que tenta encontrar a melhor linha reta que descreve a relação entre as variáveis de entrada e a variável de saída, ajustando coeficientes (pesos) para minimizar o erro.
No caso mais simples, uma rede neural com uma única camada de entrada e uma única camada de saída linear, sem funções de ativação não lineares, equivale a uma regressão linear.
Entretanto, as redes neurais se destacam por sua capacidade de modelar relações não lineares graças às funções de ativação e às camadas ocultas.
Enquanto a regressão linear é limitada a relacionamentos lineares entre variáveis, as redes neurais podem capturar padrões complexos e não lineares.
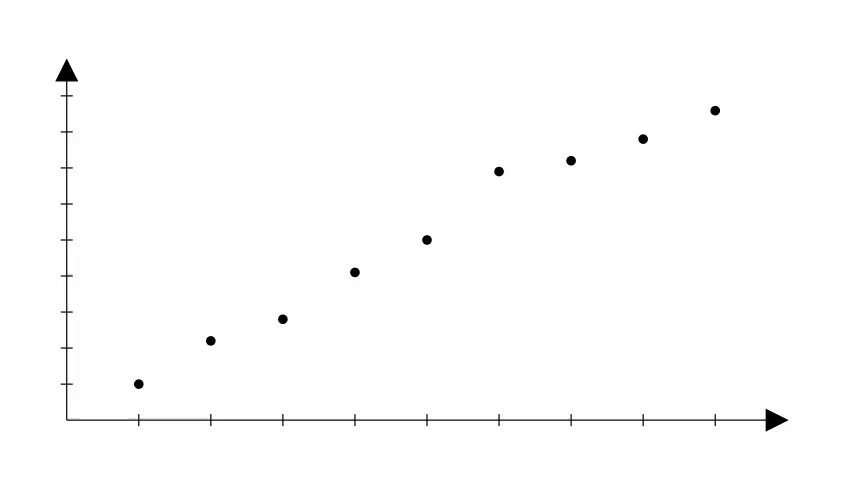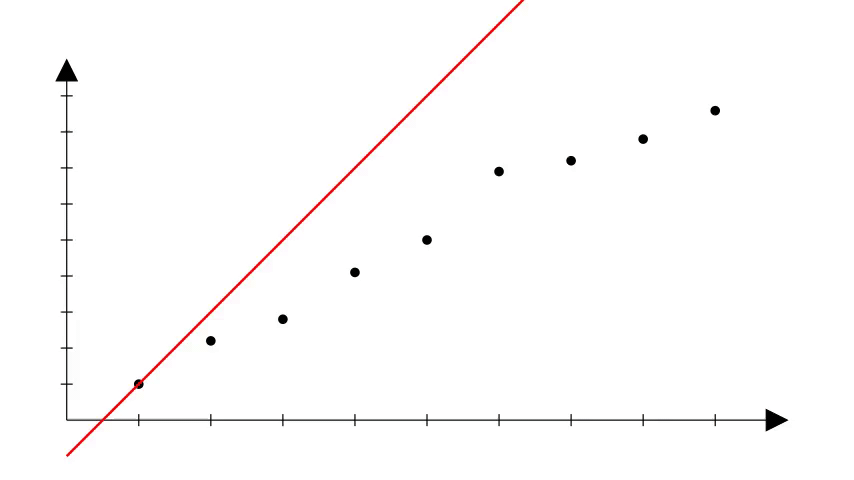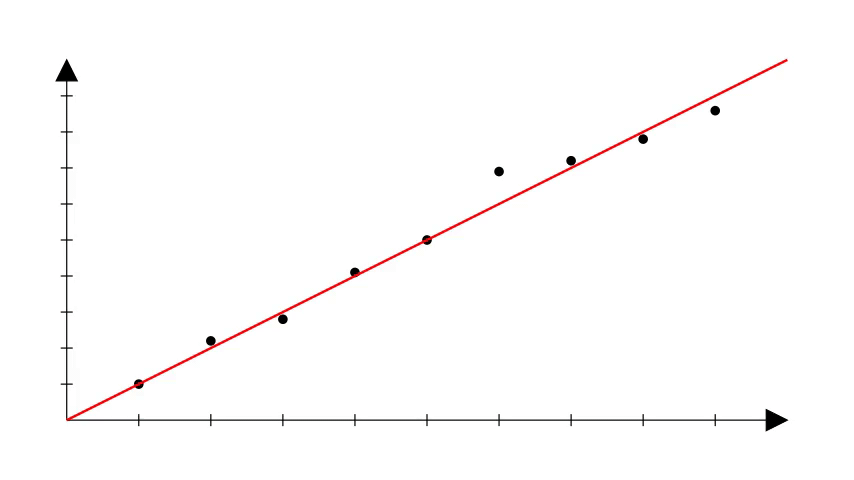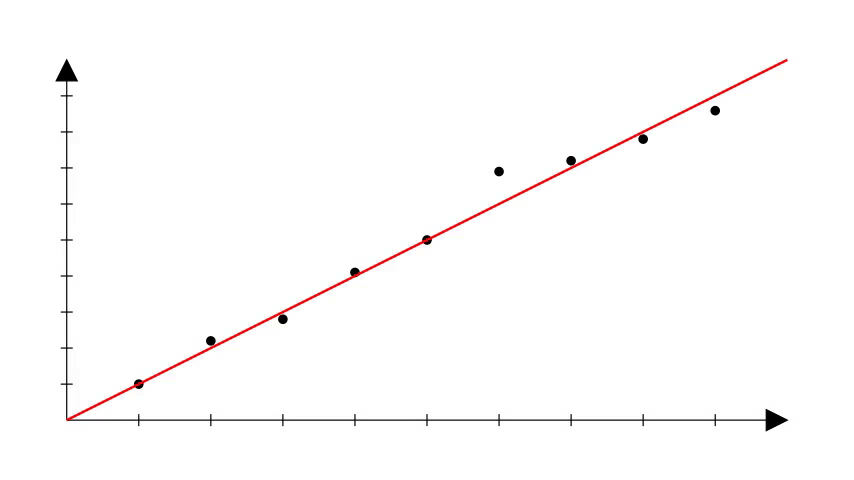
Porém, é importante notar que na regressão linear também não sabemos os coeficientes corretos que podem produzir a reta que se ajusta bem aos dados.
Uma forma de começar é escolher valores aleatórios e ir ajustando esses valores até que a reta que melhor se ajusta aos dados seja obtida.
Exemplos de aplicação
O problema que usamos como exemplo é um problema de regressão, onde estamos tentando estimar um valor contínuo relacionado a quantidade de produtos vendidos.
Porém, as redes neurais podem ser aplicadas nos mais diversos tipos de problemas. Alguns exemplos são:
| Aplicação | Descrição | Objetivo Principal | Tipo de Problema |
|---|---|---|---|
| Classificação de Imagens Médicas | Uso de redes neurais para analisar imagens como tomografias ou raios X e identificar sinais de doenças. | Atribuir cada imagem a uma categoria pré-definida, como "doente" ou "saudável". | Supervisionado (Classificação) |
| Segmentação de Clientes em Marketing | Redes neurais ajudam a encontrar padrões ocultos nos dados de clientes, agrupando-os em segmentos semelhantes. | Agrupar clientes com características similares para personalização de campanhas. | Não supervisionado (Segmentação) |
| Previsão de Séries Temporais | A rede neural processa uma sequência de dados ao longo do tempo para prever valores futuros. | Antecipar valores futuros com base em dados históricos. | Supervisionado (Regressão) |
| Redução de Dimensionalidade | Compressão de dados complexos em um espaço de menor dimensão, preservando informações relevantes. | Facilitar a análise e visualização de dados com muitas variáveis. | Não supervisionado |
Quais as vantagens e limitações das redes neurais?
As redes neurais oferecem uma série de vantagens em relação a outros métodos tradicionais de Machine Learning, especialmente em problemas que envolvem dados complexos e não lineares.
Uma das principais vantagens é sua capacidade de identificar padrões que são difíceis de modelar por abordagens mais simples, como a regressão linear.
Isso as torna ideais para tarefas como reconhecimento de imagens, processamento de linguagem natural e análise preditiva.
Além disso, as redes neurais conseguem aprender e melhorar conforme são expostas a grandes volumes de dados. Com o avanço de hardware, como GPUs, elas também são cada vez mais eficientes em tarefas que exigem processamento em tempo real, como sistemas de recomendação, direção autônoma e reconhecimento de voz.
Outro ponto positivo é que redes neurais têm uma grande capacidade de generalizar os padrões que aprendem, o que as permite fazer previsões precisas em dados que não viram durante o treinamento.
Por outro lado, as redes neurais possuem várias limitações que precisam ser consideradas.
Uma das principais é a necessidade de abundância de dados e recursos computacionais para serem eficazes, o que pode torná-las inviáveis para pequenos datasets ou situações com restrições de processamento.
O processo de treinamento também pode ser muito demorado, especialmente para redes profundas, que exigem muitas iterações e ajustes finos nos hiperparâmetros.
Outro desafio comum é o risco de overfitting, quando a rede se ajusta demais aos dados de treinamento e perde sua capacidade de generalizar para novos dados.
Além disso, redes neurais são frequentemente criticadas por sua "caixa preta", já que é difícil interpretar como elas chegam a uma determinada conclusão, o que pode ser problemático em áreas como medicina e finanças, onde a interpretabilidade é crucial.
Ajustar uma rede neural corretamente pode ser uma tarefa difícil. Encontrar a combinação certa de hiperparâmetros, como o número de camadas, a função de ativação e a taxa de aprendizado, pode exigir várias tentativas e erros.
Redes neurais também são extremamente sensíveis à qualidade dos dados de entrada, e dados ruidosos ou desbalanceados podem prejudicar seu desempenho significativamente.
Portanto, embora as redes neurais sejam extremamente poderosas, elas vêm com um conjunto de desafios que devem ser enfrentados para se obter os melhores resultados.
Conclusão
Portanto, neste artigo, estudamos o que são redes neurais e como elas funcionam. Passamos pelas seguintes etapas:
- Entendemos a estrutura de uma rede neural, desde as camadas de entrada, passando pelas camadas ocultas até a camada de saída;
- Exploramos os conceitos de pesos, bias e funções de ativação e como eles são fundamentais para o funcionamento da rede;
- Discutimos o processo de treinamento e como a rede ajusta seus pesos por meio de algoritmos como o gradiente descendente;
- Examinamos as vantagens e limitações das redes neurais, destacando sua capacidade de lidar com dados complexos e o desafio de interpretabilidade.
Com um bom entendimento sobre redes neurais, você estará mais preparado para aplicar essa poderosa ferramenta em diversos cenários, como previsões de vendas, classificação de imagens e análise preditiva em diferentes áreas.
Ficou interessado em aprender mais sobre redes neurais e suas aplicações? Recomendo que faça a formação de TensorFlow e Keras da Alura, onde um time de especialistas vai te guiar no desenvolvimento de suas habilidades, capacitando você a aplicar redes neurais em projetos do mundo real e alavancar sua carreira na ciência de dados.
Créditos
- Conteúdo: Allan Segovia Spadini
- Produção técnica: Rodrigo Dias
- Produção didática: Cláudia Machado
- Designer gráfico: Alysson Manso
- Apoio: Rômulo Henrique








