Um pouco sobre séries temporais e suas aplicações

Já parou para pensar em como os dados podem nos contar histórias fascinantes sobre o passado, presente e até mesmo o futuro?
A temperatura ao longo dos dias, semanas, meses e anos registradas em uma cidade ou um país, o desempenho do sistema de uma bolsa de valores, os seus batimentos cardíacos por minuto, o número de casos de pessoas vacinadas contra a Covid-19 com o passar do tempo, a produção mensal de uma fábrica de veículos elétricos são exemplos claros das séries temporais.
De maneira mais simplificada, séries temporais são conjuntos de dados coletados ao longo do tempo onde as observações são registradas em intervalos regulares.
Conforme citado, são dados amplamente utilizados em diversas áreas para analisar padrões, prever tendências e entender o comportamento de fenômenos ao longo do tempo.
Um breve histórico sobre séries temporais
O surgimento das séries temporais como área de estudo está associada ao desenvolvimento da estatística e da econometria, com contribuições significativas ao longo dos séculos XIX e XX com seus pioneiros.
Estatísticos como Francis Galton e Karl Pearson começaram a desenvolver métodos para analisar dados coletados ao longo do tempo. Galton – primo de Charles Darwin – foi pioneiro na aplicação de técnicas para identificar padrões em conjuntos de dados, além de ter desenvolvido métodos para analisar correlações e distribuições de dados.
Suas contribuições foram fundamentais para o desenvolvimento de métodos estatísticos essenciais na análise de séries temporais.
Paralelamente, Pearson, conhecido como o pai da estatística moderna, criou o coeficiente de correlação e outras ferramentas para descrever relações entre variáveis.
Ele foi um dos primeiros a reconhecer a importância de coletar e analisar dados ao longo do tempo para compreender padrões e tendências.
Este também foi um tema que rendeu um Prêmio Nobel de Economia para Trygve Haavelmo em 1989. Sua principal contribuição foi a aplicação de técnicas estatísticas que consideravam a natureza dinâmica para estudar relações econômicas ao longo do tempo (inferência estatística em modelos econômicos).
Os anos de 1960 e 1970 merecem um destaque na história das séries temporais pois foi durante este período que os estatísticos George Box e Gwilym Jenkins formalizaram os modelos ARMA e ARIMA.
Estes métodos revolucionários trouxeram uma estrutura matemática formal para descrever e prever este típico conjunto de dados com base em padrões observados historicamente e ainda são amplamente adotados.

Características e aplicações das séries temporais
Este conjunto de dados apresenta características próprias que o torna único em comparação com outros tipos de dados. São elas: tendência (T), sazonalidade (S), ciclo (C) e ruído (I).
A decomposição de uma série temporal é expressa matematicamente como:

Como vimos até aqui, as séries temporais representam uma ferramenta muito poderosa nas mais diversas áreas do conhecimento!
Na economia e finanças, por exemplo, as séries temporais auxiliam na previsão do PIB, da inflação e até mesmo do mercado de ações.
Na meteorologia, elas são utilizadas para prever o tempo e entender as mudanças climáticas (inclusive, podemos constatar o aquecimento global através dos dados!).
Já para a saúde pública, elas ajudam a monitorar a propagação de doenças, na previsão de epidemias e até na tendência de mortalidade e natalidade.
Mas as aplicações não param por aí! As séries temporais também são utilizadas em engenharia, marketing, transporte e muitas outras áreas.
Elas são essenciais para quem deseja entender o passado, analisar o presente e antecipar cenários futuros, fornecendo informações valiosas para a tomada de decisões estratégicas, robustas e sustentadas matematicamente.
Alguns conceitos fundamentais
As séries temporais envolvem uma variedade de fórmulas e conceitos que são fundamentais para sua análise e modelagem.
Abaixo, estão alguns dos conceitos mais comuns e importantes utilizados – exceto modelos – neste tema:
- Média Móvel Simples (MMS): A média móvel simples é usada para suavizar variações aleatórias e destacar tendências ao longo de um período específico m.

- Média Móvel Exponencial (MME): A média móvel exponencial dá maior peso aos dados mais recentes, sendo útil para capturar mudanças mais rapidamente.
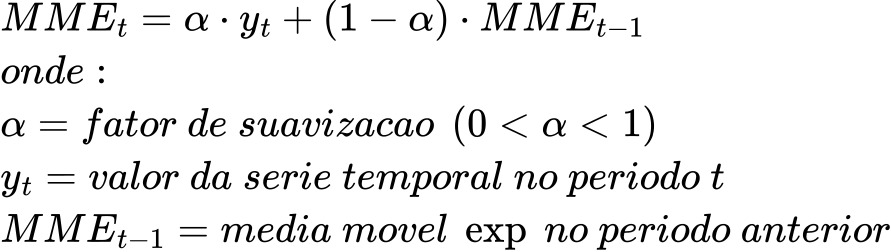
- Autocorrelação: A autocorrelação calcula o coeficiente de correlação entre a série temporal original e uma versão deslocada dela mesma por um número h de intervalos de tempo.

O valor de ρ(h) varia de -1 a 1, onde:
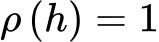
Correlação perfeita positiva (a série está perfeitamente correlacionada consigo mesma após o deslocamento h).
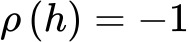
Correlação perfeita negativa.
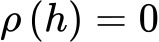
Não há correlação linear.
Cada uma dessas fórmulas captura diferentes aspectos deste conjunto de dados, desde a estrutura de autocorrelação até a presença de tendências e sazonalidades.
A escolha do modelo apropriado depende dessas características específicas e também dos objetivos da análise ou previsão temporal.
Métricas de erro
- Erro Médio Absoluto (MAE): O MAE calcula a média das diferenças absolutas entre os valores previstos e observados. Ele fornece uma medida da magnitude média dos erros de previsão.

- Erro Quadrático Médio (MSE): O MSE calcula a média dos quadrados dos erros entre os valores previstos e observados. Ele dá mais peso aos grandes erros devido ao quadrado das diferenças.

- Raiz do Erro Quadrático Médio (RMSE): O RMSE é a raiz quadrada do MSE e fornece uma interpretação na mesma escala dos dados originais. É útil para interpretar o erro de previsão em termos da unidade da série temporal.
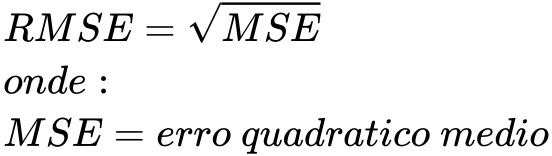
- Erro Médio Percentual Absoluto (MAPE): O MAPE calcula a média dos erros percentuais absolutos em relação aos valores observados.
É expresso como uma porcentagem, o que o torna útil para comparar o desempenho de diferentes modelos, especialmente quando as unidades dos dados variam significativamente.

A escolha da métrica de erro para séries temporais depende do contexto do problema e das características dos dados.
O MSE ou RMSE são mais apropriados quando se deseja penalizar grandes erros de forma intensa. Para interpretação em termos percentuais, o MAPE é preferível.
Bibliotecas Python
Existem várias bibliotecas Python que são utilizadas para análise e previsão de séries temporais. Aqui estão algumas:
- Função: Manipulação e análise de dados estruturados, incluindo funcionalidades específicas para séries temporais.
- Uso: Leitura e manipulação de dados temporais, resampling, agregação e visualização.
- NumPy
- Função: Computação numérica eficiente em Python.
- Uso: É fundamental para operações matemáticas rápidas e eficientes em Python, essenciais para o processamento de grandes conjuntos de dados de séries temporais.
- Statsmodels
- Função: Biblioteca que inclui modelos estatísticos, incluindo ARIMA, SARIMA.
- Uso: Ampla gama de métodos estatísticos para modelagem de séries temporais e outras análises estatísticas, com ênfase na inferência estatística.
- Scikit-learn:
- Função: Biblioteca de aprendizado de máquina geral que inclui ferramentas para pré-processamento de dados, seleção de modelos e avaliação.
- Uso: Aplicar técnicas de aprendizado de máquina supervisionado e não supervisionado em problemas de séries temporais, como previsão e classificação.
- TensorFlow / Keras ou PyTorch:
- Função: Bibliotecas de aprendizado profundo (deep learning) para construir e treinar redes neurais.
- Uso: Modelagem de séries temporais complexas usando redes neurais recorrentes (RNNs), redes neurais convolucionais (CNNs) ou modelos seq2seq.
- Prophet (Facebook):
- Função: Biblioteca desenvolvida pelo Facebook para previsão de séries temporais com sazonalidade.
- Uso: Projetado para ser uma ferramenta de previsão de séries temporais fácil de usar, permitindo modelagem automatizada de sazonalidade, feriados e tendências de longo prazo.
Essas bibliotecas oferecem uma variedade de funcionalidades desde manipulação básica de dados temporais até modelagem avançada com técnicas estatísticas e de aprendizado de máquina.
A escolha da biblioteca depende das necessidades específicas do projeto e do tipo de análise ou modelagem que se deseja realizar.
O futuro
A evolução dos métodos analíticos, impulsionada pelo aumento na capacidade computacional e pela adoção de técnicas avançadas de aprendizado de máquina e inteligência artificial, continua a expandir as fronteiras da aplicação de séries temporais em diversas disciplinas.
Em resumo, o surgimento e o desenvolvimento das séries temporais são resultado de contribuições significativas de diversos pesquisadores ao longo dos últimos séculos, moldando uma disciplina fundamental para entender e antever fenômenos.
O melhor de tudo é que, assim como o espaço-tempo, a área continua em constante expansão!
