Árvores de decisão: modelo de Machine Learning para Classificação e Regressão

Quando falamos em "árvores", a primeira coisa que vem à mente da maioria das pessoas é um organismo vivo, com raízes, tronco e galhos que se estendem em várias direções.

No entanto, quando estamos no campo da Data Science, logo nos lembramos das Árvores de Decisão.

As Árvores de decisão são cada vez mais utilizadas para tomadas de decisões e auxílio para diferentes tipos de empresa e modelos de negócio e dominar esse tema te capacita a se tornar um profissional mais completo e atualizado sobre as principais ferramentas disponíveis no mercado.

Sendo assim, neste artigo, você vai aprender sobre:

• O que é uma árvore de decisão para classificação e regressão;
• exemplos práticos sobre onde e como são aplicadas;
• e descobrir em detalhes como são feitas as escolhas das árvore de decisão, ou seja, como a árvore chegou naquele resultado?

Então, vem comigo e vamos descobrir juntos(as) como essa ferramenta funciona através da leitura desse artigo.

O que são Árvores de Decisão

As Árvores de Decisão são um tipo de modelo de Machine Learning que funciona de maneira semelhante a um fluxograma.

O modelo é estruturado em nós de decisão, onde cada nó interno representa uma condição ou regra baseada em uma variável.

Esses nós dividem os dados em grupos, tomando decisões até chegar aos "nós folha", que representam o resultado ou a previsão final.

Confira abaixo um gif que representa a estruturação de uma Árvore de Decisão com seus nós de decisão e os nós folha:

Em termos simples, uma árvore de decisão busca responder a perguntas até alcançar uma conclusão.

Podemos associar esse modelo a "fluxogramas" das tomadas de decisão que fazemos para coisas simples do dia a dia.

Por exemplo, digamos que você está pensando se consegue ou não jogar online hoje. Quais requisitos você teria que seguir para jogar esse jogo?

Podemos separar dois: se você tem internet em casa, pois sem internet não é possível jogar online, e se você tem tempo livre para realizar essa tarefa. Se você tiver internet e tempo livre, você consegue jogar online hoje, caso contrário não dá para jogar.

Veja só o fluxograma que construímos para tomar essa decisão:

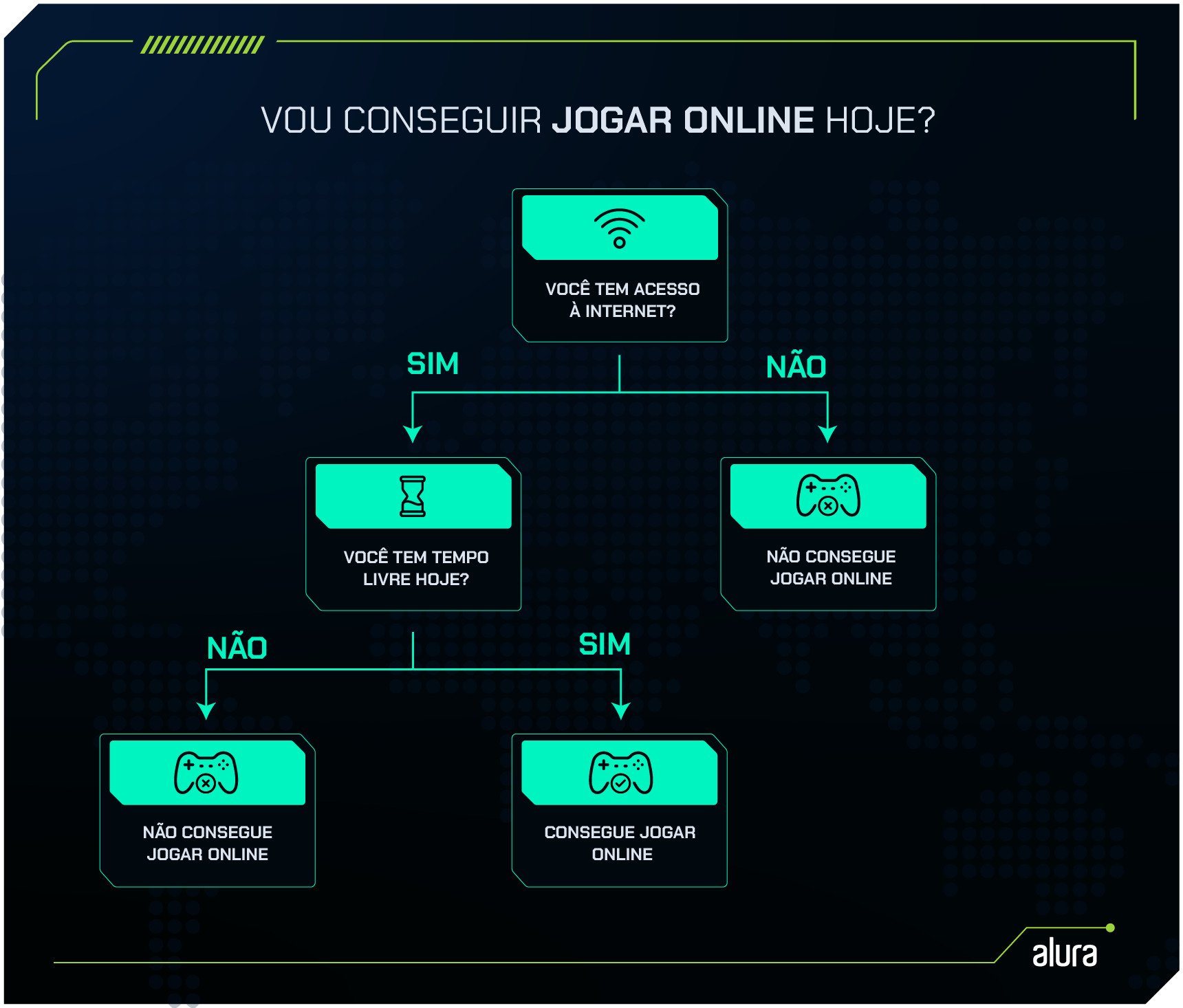
Podemos notar a estrutura de uma Árvore de Decisão nesse simples exemplo!

Na imagem, temos os nós de decisão, que são as perguntas "Você tem acesso à internet?" e "Você tem tempo livre hoje?".

Esses nós determinam os caminhos que podem ser seguidos na árvore, dependendo das respostas (Sim ou Não).

Já os nós folha representam as conclusões finais, ou seja, os resultados possíveis: "Não consegue jogar online" ou "Consegue jogar online".

Seguindo o exemplo, é possível perceber como é fácil entender a tomada de decisão apenas acompanhando o fluxograma.

Trazendo isso para o contexto de Árvore de Decisão, podemos destacar a facilidade de interpretar seu resultado como um de seus pontos fortes, pois a lógica por trás de suas decisões é visível e clara, assim como no exemplo anterior.

As Árvores de Decisão são comumente utilizadas em modelos de aprendizado supervisionado para Classificação e Regressão.

Embora possam ser aplicadas em ambos os tipos de problemas, a forma como a árvore toma decisões e interpreta os resultados apresenta diferenças entre esses dois casos.

Para compreender essas diferenças, precisamos primeiro entender o que são Classificação e Regressão.

O que é Classificação

A Classificação é um tipo de problema de aprendizado supervisionado onde o objetivo é categorizar dados em grupos ou classes predefinidas.

Um exemplo comum seria o modelo que classifica se clientes de um site estão mais propensos a comprar ou não comprar determinado produto com base em seus comportamentos de navegação, histórico de compras e outras características.

Esses modelos podem ajudar empresas a direcionar campanhas de marketing de forma mais eficiente, aumentando as chances de conversão.

Saiba mais sobre Classificação no artigo Problemas resolvidos por algoritmos de classificação.

O que é Regressão?

Por outro lado, a Regressão se concentra em prever valores contínuos, ou seja, números que podem variar dentro de um intervalo.

Diferente da classificação, o foco aqui não é atribuir uma categoria, mas prever uma quantidade ou valor.

Um exemplo seria prever o faturamento de uma loja online com base em fatores como número de clientes, tempo de permanência no site e preços dos produtos.

Esses modelos de regressão podem ajudar as empresas a fazer projeções de receita e ajustar suas estratégias de venda com base nas previsões geradas.

Qual é a diferença entre Classificação e Regressão?

Embora Classificação e Regressão sejam aplicadas em cenários de aprendizado supervisionado, elas têm objetivos diferentes.

A classificação lida com a divisão dos dados em categorias ou classes distintas, enquanto a regressão se concentra em prever valores contínuos.

Em resumo, se a tarefa é prever um rótulo (como "comprar" ou "não comprar"), estamos falando de classificação.

Se a tarefa é prever um valor numérico (como o faturamento mensal de uma loja), estamos falando de regressão.

Árvore de Decisão para classificação

Quando falamos em Árvores para Classificação, entendemos que o problema a ser resolvido envolve a previsão de categorias.

Um exemplo comum seria o de um banco que deseja decidir se aprova ou não pedidos de empréstimo com base nas características financeiras e de risco do cliente, como o valor Solicitado para o empréstimo e sua Renda anual.

Seguindo esse exemplo, podemos construir uma árvore com a seguinte estrutura:

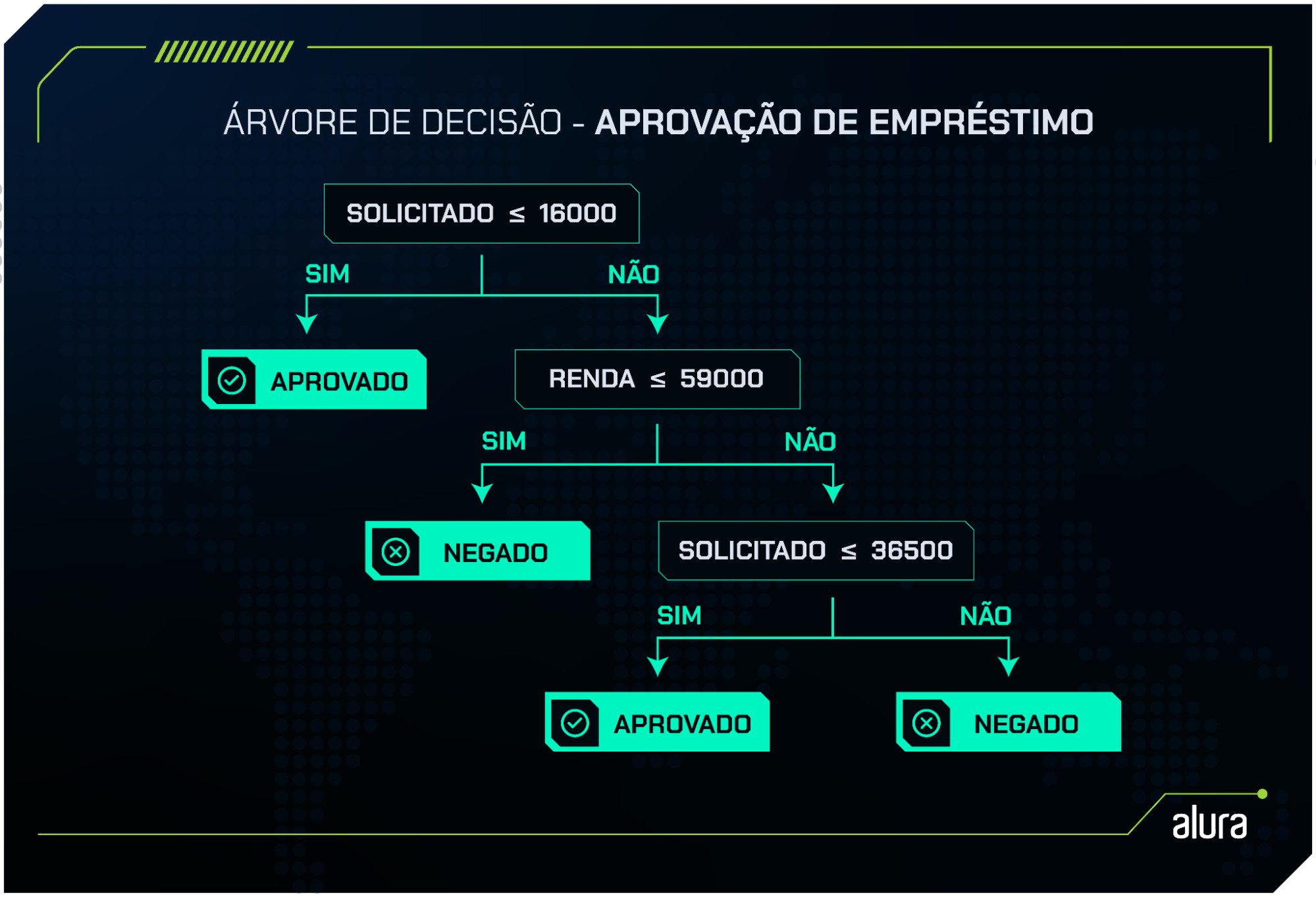
Como já apresentado anteriormente, cada Árvore de Decisão é composta por três elementos principais:

• o nó raiz, que é a primeira pergunta ou critério que divide os dados;
• os nós de decisão internos, que são as perguntas intermediárias;
• e as folhas, que representam as conclusões finais.

No exemplo, temos uma árvore com 3 nós de decisão, que separam o caminho da árvore em dois, e 4 nós folha que indicam o resultado final da solicitação de empréstimo, podendo ser "APROVADO" ou "NEGADO".

Se quisermos entender o motivo de negar ou aprovar cada solicitação, basta seguir a progressão da árvore de cima para baixo.

O primeiro nó que encontramos, localizado no topo da árvore, é um nó de decisão, também chamado de nó raiz por ser o ponto inicial. Ele separa o conjunto em dois grupos: os valores de Solicitado que são menores ou iguais a 16.000 e aqueles que são maiores.

Quando o valor Solicitado for menor ou igual a 16.000, o empréstimo é aprovado, conforme indicado no nó folha. Caso contrário, o conjunto de dados segue para outro nó de decisão.

O segundo nó faz uma nova separação, desta vez com base na Renda. Ele divide o conjunto em dois grupos: clientes com Renda menor ou igual a 59.000 e clientes com Renda superior a esse valor.

Se a Renda for menor ou igual a 59.000, o empréstimo será negado. Caso contrário, entramos em um novo nó de decisão.

No terceiro nó, a árvore faz uma última separação baseada no valor Solicitado. Solicitações com valor menor ou igual a 36.500 são aprovadas, enquanto as que excedem esse valor são negadas.

Após interpretar como a Árvore de Decisão realiza suas escolhas, é natural surgir a dúvida: Como a árvore chegou nesse resultado?

O Aprendizado na Árvore de Classificação

Durante o processo de aprendizado, a Árvore de Decisão busca dividir os dados de forma a maximizar a separação entre as classes (ou categorias).

Esse processo consiste em identificar os limites de valores para os atributos que melhor separam os rótulos dos dados, ou seja, a previsão que o modelo irá realizar, como aprovar ou negar um empréstimo.

No início, o modelo avalia todos os atributos disponíveis, no nosso exemplo seria a Renda e o valor Solicitado.

Para cada atributo, ele testa diferentes pontos de corte, ou seja, valores que podem ser usados para dividir os dados.

O objetivo é encontrar o ponto de corte que mais reduz a impureza dos grupos resultantes.

A impureza refere-se à mistura de classes dentro de um grupo de dados. Se um nó contém apenas dados de uma única classe, por exemplo, todos as solicitações são aprovadas, ele é considerado puro (impureza zero).

No entanto, se o nó contém uma mistura de classes, como algumas solicitações aprovadas e outras negadas, ele é considerado impuro.

A Árvore normalmente utiliza uma métrica chamada índice de Gini para calcular a impureza em cada nó. O índice de Gini varia de 0 (puro) a 1 (totalmente impuro).

Por exemplo, um nó contendo apenas clientes com empréstimos aprovados teria impureza de 0, enquanto um nó com uma mistura equilibrada de clientes aprovados e negados teria uma impureza maior.

Ao construir uma árvore de decisão, o algoritmo calcula a impureza de Gini para cada atributo e escolhe aquele que melhor separa as classes, ou seja, o que resulta em nós mais puros e o atributo que minimiza a impureza é escolhido como o nó raiz.

Em seguida, a árvore repete o processo nos ramos subsequentes até que não seja mais possível melhorar a separação dos dados ou até que um critério de parada seja atingido.

Ainda no exemplo de concessão de empréstimos, construímos um pequeno conjunto de dados para montar um modelo e verificar os valores de impureza catalogados:

Renda	Solicitado	Aprovacao
50000	15000	1
60000	30000	1
45000	12000	1
50000	40000	0
75000	35000	1
35000	20000	0
40000	10000	1
120000	50000	0
65000	38000	0
47000	14000	1
58000	36000	0
35000	17000	0

Dentro do conjunto temos as características de Renda e Solicitado, o rótulo dos nossos dados estão na coluna Aprovacao, sendo o resultado 1 como aprovado, e 0 como negado. Note que, nesse exemplo, iremos utilizar um pequeno conjunto de apenas três colunas (características e alvo) para facilitar o ensino e aprendizagem. Mas modelos dessa natureza lidam com dados muito maiores e com múltiplas características.

Abaixo a Árvore de Decisão final feita com Python:

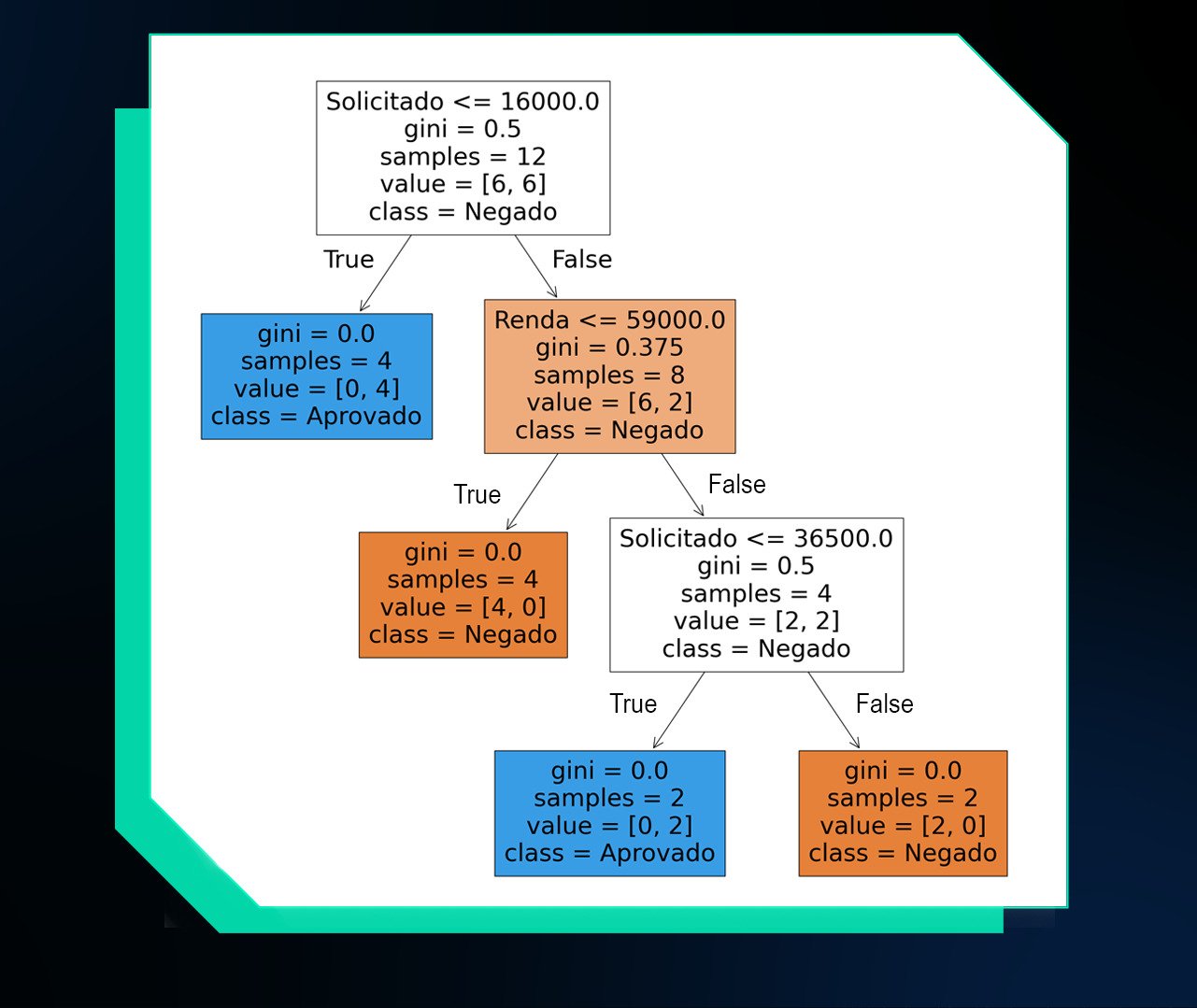
Nessa imagem, podemos observar as divisões dos dados em nós de decisão, juntamente com a quantidade de amostras separadas e os valores do índice de Gini para cada nó.

Nos nós folha, temos a apresentação do índice de Gini igual a zero, o que indica pureza máxima.

Isso significa que todas as amostras daquele nó pertencem a uma única classe, ou seja, todos os exemplos de treinamento foram corretamente separados como Aprovado ou Negado.

Isso ocorre porque não há mais mistura de classes nessas folhas: cada uma contém apenas exemplos de uma classe específica.

Confira o código usado para reproduzir esse exemplo nesse repositório do Github.

Árvore de Decisão para regressão

A Árvore de Decisão para problemas de regressão mantém a mesma estrutura básica da árvore usada para classificação: ela começa com um nó raiz, que é o ponto de decisão inicial, e, ao longo do caminho, faz divisões sucessivas até chegar aos nós folha, que contêm os resultados finais.

No entanto, a principal diferença entre a árvore de regressão e a de classificação está nos resultados.

Enquanto na classificação os resultados são categorias (como "Aprovado" ou "Negado"), na regressão os resultados são valores numéricos contínuos.

Isso significa que a árvore de regressão é usada para prever valores como preços, temperaturas, ou quantidades, em vez de classes.

Outra diferença significativa está na métrica de avaliação usada durante o aprendizado.

Como os resultados são valores contínuos, o índice de Gini, utilizado em árvores de classificação, não é adequado para medir a qualidade das divisões.

Em vez disso, a árvore de regressão utiliza métricas como o Erro Quadrático Médio para avaliar o quão bem as divisões estão prevendo os valores numéricos.

O objetivo é minimizar esse erro, de forma que as previsões fiquem o mais próximo possível dos valores reais.

Um exemplo comum do uso de Árvore de Regressão é quando uma rede de supermercados busca prever quantos produtos serão comprados com base em uma característica como o preço do produto, ajudando a planejar melhor seu catálogo de ofertas. Vejamos um pequeno conjunto de dados que reflete essa situação:

Preço	Quantidade
18.8	108
20.7	72
22.99	94
36.99	10
39.99	13
41.2	18
50.5	31
68.2	35
80.4	49

É importante lembrar que, no mundo real, esses modelos são utilizados com conjuntos de dados muito maiores e mais complexos. No entanto, estamos utilizando esse exemplo simples para facilitar o entendimento do conceito de regressão.

Ao treinar uma Árvore de Regressão com esses dados, obtemos o seguinte resultado:

Até aqui, já entendemos o conceito de nós de decisão e nós folha. Então, vamos focar nos nós folha da imagem, que são os resultados finais da árvore.

Diferentemente de uma árvore de classificação, em que os nós folha retornam categorias, em uma árvore de regressão os nós folha fornecem valores contínuos, como a quantidade estimada de produtos a serem vendidos.

Ao comparar os resultados da árvore com os dados originais, notamos que os valores estimados pela árvore nem sempre correspondem exatamente aos dados reais.

Por exemplo, quando o preço é menor que 29.99, a árvore estima que a quantidade vendida será 91.33, embora os valores reais variem. O mesmo acontece com outros intervalos de preço. Isso significa que o modelo está errado?

Na verdade, o modelo não está "errado". O que ele faz é representar a média dos valores de treinamento dentro de cada intervalo de preço.

Esse comportamento é característico do processo de aprendizado de uma árvore de regressão, que tenta generalizar a relação entre as variáveis (neste caso, preço e quantidade) para fazer previsões mais robustas e aplicáveis a novos dados.

Assim, a árvore não devolve o valor exato, mas uma aproximação baseada nas médias dos dados que ela processou.

O Aprendizado na Árvore de Regressão

Durante o processo de aprendizado, o modelo busca identificar os melhores pontos para dividir os dados, criando os nós de decisão. Esses pontos de separação são escolhidos com base no valor do Erro Quadrático Médio (MSE).

O Erro Quadrático Médio é uma métrica que avalia a diferença entre os valores reais dos dados e os valores previstos pelo modelo.

Ele é calculado a partir dos resíduos, que são as diferenças entre os valores observados nos dados e os valores previstos pela árvore.

Cada resíduo é elevado ao quadrado, para garantir que diferenças positivas e negativas não se cancelem, e esses valores são somados.

Em seguida, essa soma é dividida pelo número total de observações, resultando no valor do Erro Quadrático Médio.

O objetivo da árvore é encontrar as divisões que minimizem o Erro Quadrático Médio. Quanto menor o erro, mais próximas estão as previsões feitas pelo modelo dos valores reais.

Dessa forma, o modelo testa várias divisões possíveis e adota aquelas que resultam no menor MSE, garantindo previsões mais precisas.

O problema da busca pelo menor valor possível de (MSE) é que, se não houver controle, a árvore tentará reduzir o erro ao máximo, buscando um MSE igual a 0`, o que significa que os valores previstos seriam exatamente iguais aos valores reais.

Embora isso possa parecer ideal, na prática, a árvore faz tantas divisões que acaba criando um nó para cada exemplo específico nos dados de treinamento. Isso gera uma árvore complexa, cheia de nós de decisão, onde cada nó folha corresponde a um único valor. Esse fenômeno é chamado de sobreajuste.

Sobreajuste em Árvores

O sobreajuste (ou overfitting) ocorre quando o modelo se ajusta excessivamente aos dados de treinamento, capturando até mesmo o "ruído" ou variações irrelevantes dos dados, em vez de aprender padrões generalizáveis.

Em outras palavras, o modelo se torna tão detalhado que consegue prever perfeitamente os dados de treinamento, mas perde a capacidade de fazer boas previsões em novos dados.

Isso porque o modelo, ao tentar prever com extrema precisão os valores já conhecidos, não consegue generalizar adequadamente quando recebe novos dados.

No caso das Árvores de Regressão, o sobreajuste pode acontecer quando a árvore realiza muitas divisões para minimizar o erro, resultando em nós folhas que contêm apenas uma amostra.

Assim, cada divisão especifica apenas um valor observado nos dados de treinamento, o que prejudica a capacidade do modelo de prever valores fora desse conjunto.

Para evitar o sobreajuste é importante limitar a complexidade do modelo. Uma das táticas mais comuns é restringir a profundidade da árvore, que representa o número de divisões que podem ser feitas desde o nó raiz até o nó folha.

Quanto maior a profundidade, mais complexa será a árvore, e maior a chance de sobreajuste.

Além disso, podemos limitar o número máximo de nós folha ou aumentar o número mínimo de amostras que um nó deve conter antes de ser dividido.

Outra estratégia é aumentar o número mínimo de amostras em um nó folha, garantindo que cada divisão represente um grupo maior de dados.

No exemplo da previsão de quantidade com base no preço, limitamos a árvore para que cada nó folha tenha, no mínimo, 3 amostras.

Isso ajudou a evitar o sobreajuste, forçando a árvore a generalizar melhor. O resultado dessa árvore, gerada com Python, pode ser visto abaixo:

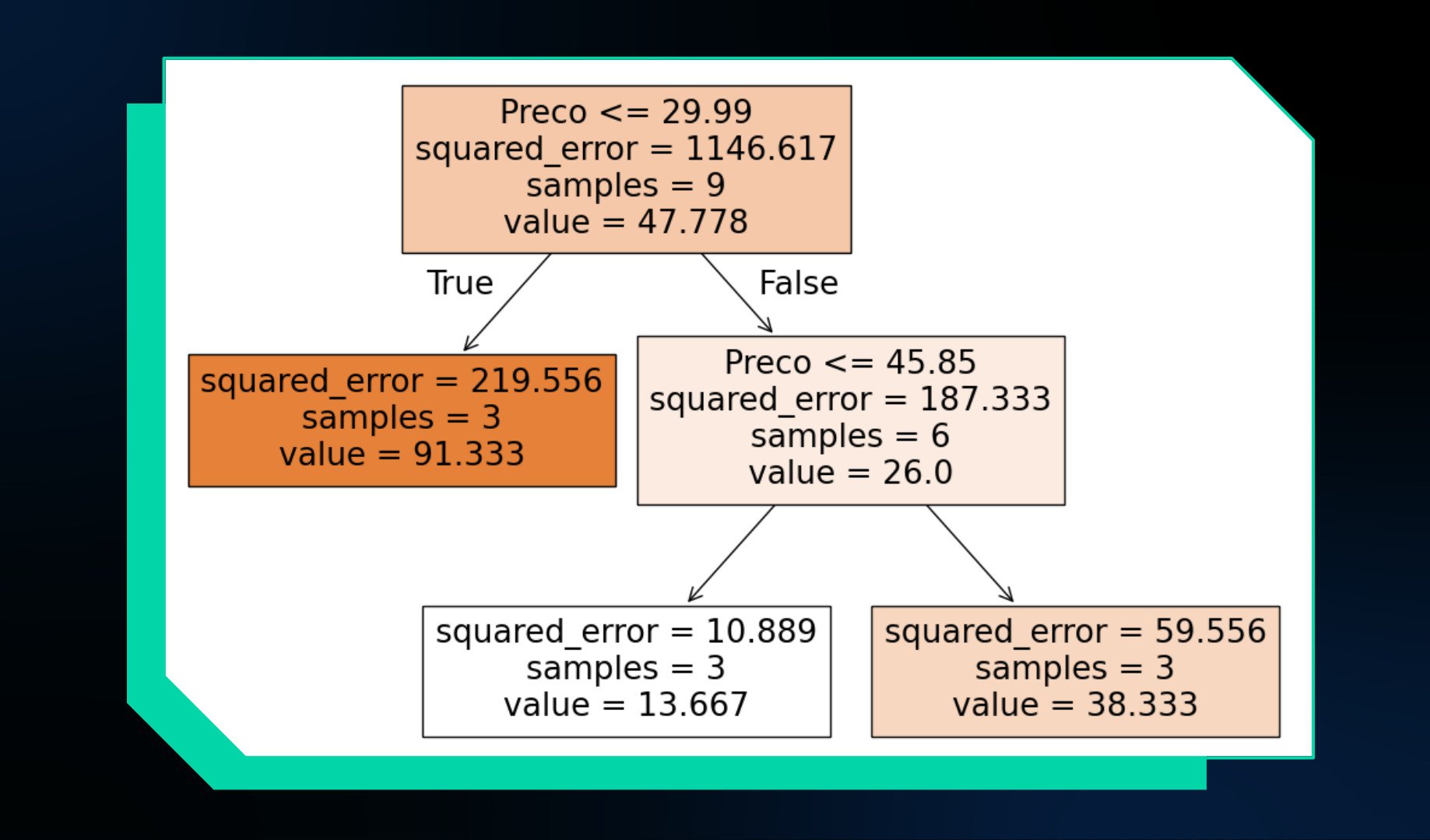
Confira o código usado para reproduzir esse exemplo nesse repositório do Github.

Conclusão

Neste artigo, entendemos como as Árvores de Decisão são utilizadas em casos de classificação e regressão. Durante a leitura, fomos capazes de:

• Entender o conceito de árvore de decisão e suas aplicações;
• Compreender as diferenças entre problemas de classificação e regressão;
• Identificar como as árvores de decisão tomam decisões baseadas em atributos;
• Explorar como o modelo de árvore de decisão é eficaz na previsão de categorias ou valores contínuos;
• Compreender os conceitos de impureza, resíduo e sobreajuste no contexto de árvores de decisão.

Deseja colocar em prática os conteúdos aprendidos neste artigo e se aprofundar nesses conceitos e muitos outros?

Confira nossas formações de Machine Learning como a Formação Machine Learning com Python: Classificação, Formação Machine Learning com Python: Regressão e Formação Machine Learning na prática: fundamentos e aplicações.

Até mais!

Créditos

• Conteúdo: Mirla Costa
• Produção técnica: Rodrigo Dias
• Produção didática: Tiago Trindade
• Designer gráfico: Alysson Manso
• Apoio: Rômulo Henrique