Quais os algoritmos de clusterização e quando utilizar?

A análise de agrupamentos representa um conjunto de técnicas exploratórias muito eficientes para verificar a existência de comportamentos semelhantes entre registros de um conjunto de dados e com objetivo de formar grupos que possuem características similares.
Estes grupos também são conhecido como clusters, portanto, a análise de agrupamentos também pode ser chamada de clusterização.
Pensando nisso, neste artigo, vamos explorar os principais algoritmos de clusterização, suas diferenças e quando utilizá-los. Para isso, vamos conferir os seguintes algoritmos:
- K-Means
- DBSCAN
- Mean Shift
- e, por fim, a técnica de Clusterização hierárquica
Vamos lá?
Como funciona a técnica de clusterização
O primeiro ponto importante é que uma das principais vantagens das técnicas de clusterização é rotular os dados com informações que desejamos prever. Isto é, a análise é de caráter exploratório.
Existem inúmeras técnicas e com diferentes critérios para definir a similaridade entre os dados e formar os grupos.
Essas técnicas servem para as mais diversas áreas, como sistemas de recomendação, segmentação de clientes e detecção de anomalias.
Os critérios de semelhança e dissimilaridade destas técnicas geralmente envolvem o cálculo de distância entre os registros da base de dados. Portanto, só podem ser utilizadas informações binárias (0 ou 1) ou numéricas na avaliação de semelhança.
Além disso, por conta dos cálculos de distância, esses algoritmos são muito sensíveis à presença de outliers e da diferença de escala entre as variáveis da base de dados.
Com isso dito, vamos explorar nosso primeiro algoritmo que é K-Means.

K-Means
O algoritmo K-Means é um dos algoritmos de clusterização mais populares e que tem como tarefa dividir um conjunto de dados em k grupos distintos.
O objetivo deste algoritmo é minimizar a variância dos dados dentro de cada cluster. Em outras palavras, o objetivo é maximizar a similaridade entre os pontos dentro de um cluster e maximizar a divergência de características entre clusters diferentes.
O algoritmo K-Means funciona basicamente da seguinte forma:
- É definido uma quantidade inicial de clusters em que serão divididos os dados e demarcada a posição dos centróides. Os centróides são pontos representativos de um agrupamento, geralmente na posição central dos pontos.
- O algoritmo calcula a distância de cada ponto até cada centróide e atribui ao ponto um grupo referente ao centróide mais próximo.
- Após a definição dos grupos iniciais, cada centróide é reposicionado na posição média dos pontos de cada cluster.
- Os dois passos anteriores são repetidos até que não haja variação na posição de cada cluster e atribuição de grupos de cada ponto.
A visualização abaixo representa o processo iterativo do K-Means com 3 clusters, com a definição da posição dos centróides iniciais e o reposicionamento deles com base no ponto médio dos pontos:

Quando utilizar o K-Means
- Quando se tem um grande conjunto de dados e o número de clusters k é conhecido ou pode ser estimado.
- Quando se procura uma solução rápida e eficiente para agrupar os dados.
- Quando a distribuição dos dados é aproximadamente esférica, já que como o cálculo de distância é feito de um centro para cada ponto, geralmente os grupos formados terão formato esférico/circular.
DBSCAN
O DBSCAN é um algoritmo de clusterização que se baseia na densidade dos pontos.
Com isso, essa técnica agrupa pontos próximos uns aos outros em clusters e ignora regiões onde a densidade de pontos é baixa. Ou seja, quando os pontos estão muito espaçados entre si.
Ele é capaz de identificar clusters de forma arbitrária, sem a necessidade de definir anteriormente a quantidade de grupos a serem formados e é pouco prejudicado pela presença de outliers.
Para que o algoritmo DBSCAN possa funcionar, é preciso definir um valor épsilon (ε) que determina a distância máxima a ser considerada para agrupar dois pontos em um mesmo cluster.
Outro parâmetro a ser definido é o número mínimo de pontos dentro de uma vizinhança para que o cluster possa ser definido.
O processo de geração dos clusters pelo algoritmo funciona da seguinte maneira:
- É selecionado aleatoriamente um ponto da base de dados.
- O cálculo de distância de uma esfera com raio épsilon (ε) é feito em torno do ponto selecionado.
- Caso exista, dentro da esfera, uma quantidade de pontos mínima estipulada inicialmente, os pontos dentro da esfera serão parte de um cluster. Caso contrário, o ponto será considerado um ruído.
- O processo é repetido para os pontos que foram atribuídos ao cluster até que a condição não seja mais satisfeita. Quando isso ocorrer, um novo ponto é escolhido aleatoriamente, para definir um novo cluster ou ruído.
A visualização abaixo representa o processo iterativo do DBSCAN. Em cada um dos pontos é formado um círculo de tamanho épsilon (ε) e é verificado se existem pelo menos 3 pontos nessa vizinhança. Caso existam, os pontos são alocados em um cluster:

Quando utilizar o DBSCAN:
- Quando os clusters têm formas complexas, diferentes do formato esférico.
- Quando os dados contêm ruídos e outliers.
- Quando não é possível definir a quantidade de agrupamentos a ser formada pelo algoritmo.
Mean Shift
O Mean Shift é um algoritmo que se baseia em centróides, assim como é feito no K-Means. No entanto, ele irá encontrar automaticamente a quantidade de clusters, portanto, não é necessário definir de antemão esta quantidade.
Ele é baseado na ideia de encontrar máximos locais na densidade de pontos para descobrir os centros dos clusters.
Ele funciona atualizando os candidatos a centróides para serem a média dos pontos dentro de uma determinada região.
Os candidatos a centróides são filtrados para eliminar pontos duplicados ou pontos muito próximos, formando assim um conjunto final de centróides.
O tamanho da região a ser pesquisada é determinado por um parâmetro bandwidth ou largura de banda, sendo possível definir manualmente ou de maneira automática a partir de uma estimativa.
A visualização abaixo representa o processo iterativo do Mean Shift. Primeiramente são alocados diferentes possíveis centróides e a partir do cálculo de obtenção de um valor máximo, conhecido como "hill climbing" ou subida de colina, os centróides são realocados cada vez mais próximos do valor máximo de densidade até que seja definido o centro de um cluster:
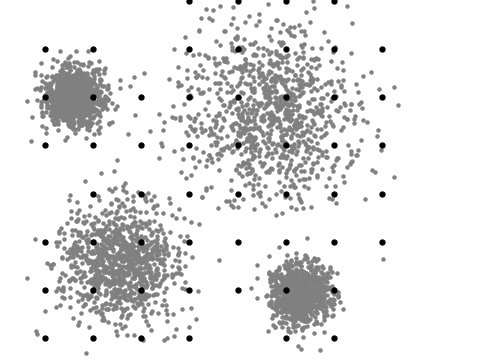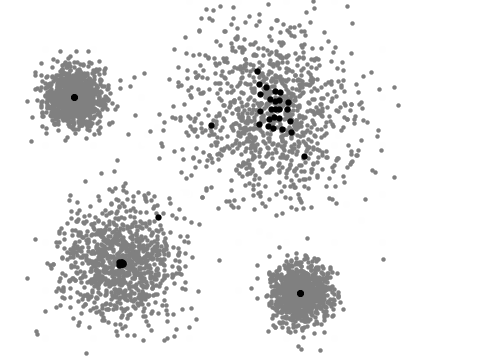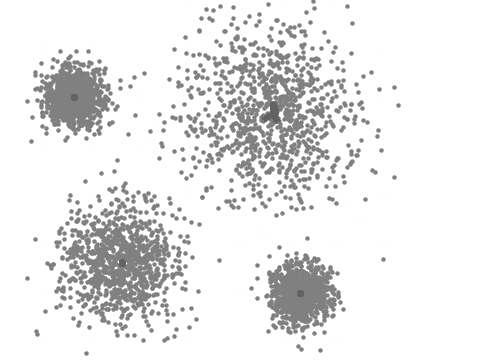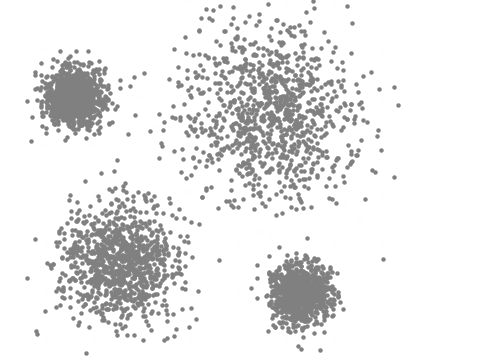
Quando utilizar o Mean Shift:
- Quando não é possível definir a quantidade de agrupamentos a ser formada pelo algoritmo.
- Quando os clusters têm formas e tamanhos arbitrários.
- Quando a base de dados não tiver muitas linhas ou não tiver muitas variáveis. O algoritmo Mean Shift é muito custoso do ponto de vista computacional e quando está trabalhando com muitas variáveis, pode não convergir muito bem nas iterações.
Clusterização hierárquica
A clusterização hierárquica é uma técnica muito eficiente para determinar a quantidade de clusters e ter uma visualização geral de como os dados estão se aglomerando.
Cada uma das observações começa em seu próprio cluster e, em seguida, clusters são sucessivamente mesclados com base na similaridade dos dados.
Essa similaridade é calculada a partir de uma métrica de distância, como a euclidiana.
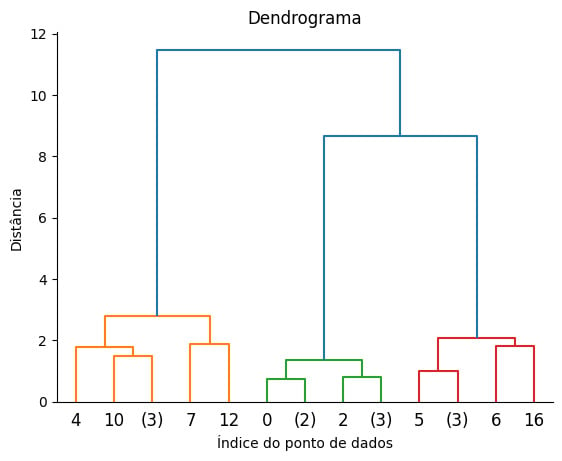
No final de todo o processo de iteração, este algoritmo produz uma visualização em forma de árvore hierárquica de clusters, chamada dendrograma.
A partir do dendrograma, é possível identificar quais dados são mais similares entre si e qual a quantidade de clusters em que os dados serão divididos.
A imagem abaixo é uma representação de um dendrograma, no qual os dados foram divididos em 3 clusters, nas cores laranja, verde e vermelho.
O eixo y representa a distância de um registro a outro, fazendo com que pontos mais próximos estejam em um mesmo cluster e pontos mais distantes estejam em clusters diferentes:
Quando utilizar a clusterização hierárquica:
- Quando se deseja visualizar a estrutura hierárquica dos dados.
- Quando não se sabe o número ideal de clusters.
- Quando os clusters têm formas e tamanhos arbitrários.
Conclusão
Neste artigo, foi possível conferir os seguintes algoritmos da clusterização, suas diferenças e quando podemos utilizá-los:
- K-Means
- DBSCAN
- Mean Shift
- e a técnica de Clusterização hierárquica
É importante ressaltar que cada algoritmo possui suas próprias vantagens e limitações, e a escolha do algoritmo correto depende da natureza dos dados e dos objetivos da análise.
Por fim, caso queira aprofundar ainda mais seus estudos nos conteúdos deste artigo, sugiro a nossa Formação Machine Learning em que um time de especialistas vai te ajudar a alavancar ainda mais sua carreira e capacitar você a adquirir cada vez mais conhecimento na área.
Um abraço e até mais.
Referências
- Documentação oficial scikit-Learn: seção Clustering
- Livro: Manual de análise de dados
- Artigo: Clustering with Scikit with GIFs
Créditos
- Criação textual: João Miranda
- Produção técnica: Rodrigo Dias
- Produção didática: Tiago Trindade
- Designer gráfico: Alysson Manso
- Apoio: Rômulo Henrique