Estatística descritiva: o que é e quais os tipos de medidas de tendência central

A estatística descritiva trata de resumir e sintetizar dados brutos.

Se quisermos respostas para perguntas sobre a vida, o universo e tudo mais, é imprescindível observar e explorar a realidade como ela é.

Acontece que a realidade é super complexa e está sempre se transformando!

Para responder, por exemplo, sobre como é a saúde econômica da população do Brasil, podemos fazer uma lista com o que cada habitante maior de idade recebe e seus respectivos gastos com itens essenciais (alimentação e moradia, por exemplo) e número de dependentes.

Esses seriam dados brutos sobre os 216 milhões de habitantes do país, com informações valiosas contidas neles.

Porém, observar cada um desses dados, individualmente, é uma tarefa praticamente impossível e, ao final, a pessoa estaria tão cansada que nem lembraria mais do que viu na primeira página (e, com certeza, muitos dos habitantes teriam algum tipo de alteração na renda nesse intervalo de tempo).

Para resolver problemas como esse é que serve a estatística descritiva: uma ferramenta matemática e social poderosa para compreender melhor a realidade em que vivemos.

Nesse artigo, vamos conversar sobre conceitos da estatística descritiva e como podemos a utilizar para chegar a números simples que comuniquem informações sobre situações complexas, e como garantir que essas informações sejam o mais verdadeiras possíveis.

Conceitos principais: o que é estatística descritiva

A estatística descritiva é o ramo da estatística que se ocupa de descrever alguma coisa. A essa coisa, chamamos variável: qualquer grandeza que esteja sendo observada e investigada.

As variáveis podem ser divididas em dois tipos principais, que também determinam o tipo de dado que será coletado:

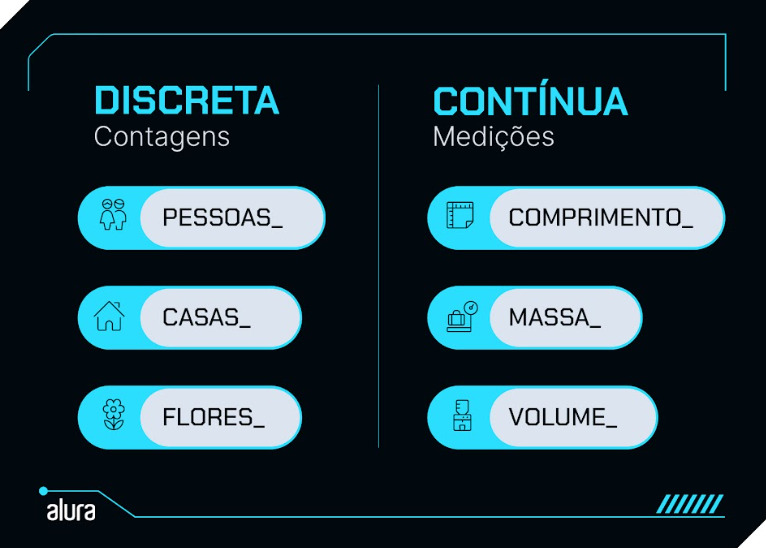
• Quantitativas: representam algo que pode ser contado ou medido.
• Discretas: quando o objeto de observação é contabilizado por unidade. Como “uma pessoa”, “cinco restaurantes”, “dez pratos”.
• Contínuas: quando o objeto de observação tem uma unidade de medida que pode assumir infinitos valores dentro de um intervalo específico, como em “metros” ou “litros”. Entre 1 e 2 litros, podemos ter 1.100, 1.3524, 1.99999 e assim por diante.

• Qualitativas ou Categóricas: Representam características ou categorias, e não números diretamente. Essas variáveis produzem dados categóricos que podem ser descritos por frequência ou proporção. Podem ser:
  • Ordinais: Quando podem ser categorizadas, como ou "opinião sobre um serviço" (bom, médio, ruim) ou nível de ensino (fundamental, médio, superior).
  • Nominais: Quando são apenas características e não tem ordem definida. Como gênero, cor dos olhos, etnia, etc.

Entender o tipo de variável é essencial porque ele define o tipo de dado que será coletado (quantitativo ou qualitativo) e também influencia as ferramentas estatísticas que podemos usar para analisá-lo.

As variáveis não existem sozinhas: elas fazem parte de um universo e precisam ser coletadas.

No exemplo sobre a saúde econômica dos brasileiros, temos que o universo é o Brasil. A população será a totalidade de pessoas que compõem esse universo.

A cada dez anos, o IBGE (Instituto Brasileiro de Geografia e Estatística) faz um estudo chamado censo.

Esse tipo de estudo é quando dados de toda a população são coletados e descritos. Um censo pode ser feito em qualquer tipo de população, seja de pessoas em um país, plantas em um bioma, produtos em uma fábrica, etc.

Porém, esse é um processo bastante custoso. Requer planejamento estratégico, recursos financeiros e disponibilidade de tempo.

Quando coletar dados de toda a população é inviável, se utiliza um estudo amostral. Nesse caso, apenas uma parcela da população é coletada de forma a representar o todo.

Ou seja: essa amostra não deve ser escolhida de forma totalmente aleatória: ela precisa ser planejada para garantir que as características principais da população sejam refletidas nela.

Por exemplo, em um estudo sobre a população brasileira, seria importante que a amostra incluísse pessoas de diferentes faixas de renda, regiões do país e idades.

Dessa forma, podemos extrair conclusões confiáveis com base em um grupo menor de dados.

Medidas de tendência central

Entendemos os tipos de dados e de onde eles vêm. Porém, como resumimos tudo isso em informações claras e úteis?

As medidas de tendência central ajudam a identificar pontos de equilíbrio nos dados. Cada uma delas tem sua importância.

Média

A média é o valor que resulta da soma de todos os dados (quando são quantitativos) dividida pelo número total de observações.

Ela é super útil quando os dados são equilibrados, mas pode ser enganosa se houver a presença de dados muito discrepantes - é preciso interpretá-la com cautela.

Vamos utilizar uma lista de salários como exemplo. Considere que os valores estão em milhares de reais. Vou compartilhar com você o código em Python e em R, escolha qual prefere testar.

Python

import numpy as np
# Lista com os salários
salarios = [3, 5, 7, 5, 8, 12, 5, 10, 15, 20]
# Média
media = np.mean(salarios)
print(f"Média: {media}")

R

# Criar um vetor com os salários
salarios <- c(3, 5, 7, 5, 8, 12, 5, 10, 15, 20)
# Média
media <- mean(salarios)
print(paste("Média:", media))

Temos o resultado 9, que é coerente. Os dados se movimentam mais ou menos em torno desse número, tanto para mais quanto para menos.

Porém, vamos fazer uma pequena alteração - substituímos o valor mais alto, 20, por 200.

Python

salarios_outlier = [3, 5, 7, 5, 8, 12, 5, 10, 15, 200]
media_outlier = np.mean(salarios_outlier)
print(f"Média com outlier: {media_outlier}")

R

salarios_outlier <- c(3, 5, 7, 5, 8, 12, 5, 10, 15, 200)
media_outlier <- mean(salarios_outlier)
print(paste("Média com outlier:", media_outlier))

A média é 27, que não representa de forma alguma o comportamento comum dos salários nessa amostra que, na maioria, estão abaixo de 10. Isso mostra como a média, sozinha, pode levar a interpretações equivocadas.

Mediana

A mediana é o valor que separa a metade inferior da metade superior de um conjunto de dados, quando eles estão organizados em ordem crescente.

Ela é muito menos influenciada por valores extremos e representa melhor a "tendência central" em casos com outliers.

Python

mediana_outlier = np.median(salarios_outlier)
print(f"Mediana com outlier: {mediana_outlier}")

R

mediana_outlier <- median(salarios_outlier)
print(paste("Mediana com outlier:", mediana_outlier))

Mesmo com o valor 200 na lista de salários, o valor da mediana é 7.5 - podemos confiar que pelo menos 50% dos valores estão abaixo de 7,5 e é provável que os valores a seguir não estejam tão distantes desse número.

Talvez você tenha percebido que o valor 7.5 não está na lista de salários. Isso acontece porque nossa lista tem um total par de itens.

Quando o total de observações é ímpar, calcular a mediana é simples: basta organizar os valores em ordem crescente e pegar o que está exatamente no meio. Por exemplo, em [3, 5, 7, 8, 12], o valor do meio é 7, então a mediana é 7.

Mas, quando o total de observações é par, a mediana é calculada como a média dos dois valores centrais. Considere a lista [3, 5, 7, 8, 12, 15]. Aqui, os dois valores centrais são 7 e 8. Para calcular a mediana, fizemos a média deles.

Isso explica por que, no exemplo anterior com os salários e o outlier 200, a mediana foi 7.5 - ela é a média dos dois valores centrais, que continuam representando bem o comportamento típico dos dados, mesmo na presença de extremos.

A mediana, portanto, é a aliada ideal para resumir conjuntos de dados onde há valores muito discrepantes ou quando precisamos de uma medida robusta que não seja influenciada por extremos.

No entanto, ela também tem limitações: não considera diretamente todos os valores do conjunto, o que pode levar à perda de informações mais detalhadas.

Moda

A moda é a medida de tendência central que indica o valor mais frequente em um conjunto de dados.

Em situações em que há repetições significativas, a moda pode ser útil para capturar padrões que nem a média nem a mediana conseguem expressar. Vamos voltar ao exemplo dos salários.

Python

from scipy import stats
moda = stats.mode(salarios)
print(f"Moda: {moda.mode[0]}, com frequência: {moda.count[0]}")

R

moda <- as.numeric(names(sort(table(salarios), decreasing = TRUE)[1]))
frequencia <- sort(table(salarios), decreasing = TRUE)[1]
print(paste("Moda:", moda, "com frequência:", frequencia))

Neste caso, a moda é 5, já que aparece com mais frequência na lista. Isso sugere que o valor 5 é comum no conjunto de dados.

No entanto, a moda também possui limitações. Se os dados forem muito variados e não houver repetições significativas, ela pode não ser uma medida informativa.

Além disso, quando existem múltiplos valores com a mesma frequência, o conjunto pode ter moda múltipla, complicando a interpretação.

A moda pode ser utilizada em dados qualitativos, também, já que reflete a frequência com que determinado dado aparece.

O perigo de confiar cegamente nas estatísticas

Os exemplos acima mostram como diferentes medidas de tendência central podem contar histórias diferentes sobre os dados.

Mas o que acontece se confiarmos em uma única medida sem analisar o contexto? Podemos tomar decisões mal informadas ou enviesadas.

Imagine que o salário médio de uma empresa é divulgado como 27 mil reais (sim, a média com outlier do exemplo anterior).

Esse valor pode criar a falsa impressão de que a maioria dos funcionários ganha muito bem.

Na realidade, a mediana (7.5 mil reais) e a moda (5 mil reais) contam uma história muito diferente: a maioria dos funcionários ganha valores significativamente menores do que a média sugere.

Isso nos leva a duas lições importantes:

1. Nenhuma medida é perfeita. A escolha da medida certa depende da natureza dos dados e do objetivo da análise. Por isso, é crucial considerar mais de uma medida sempre que possível.
2. Dados extremos (outliers) precisam de atenção especial. Eles podem ser indicativos de erros de coleta, fenômenos raros ou simplesmente variações naturais, mas, em todos os casos, precisam ser analisados cuidadosamente para evitar interpretações equivocadas.

Essas reflexões nos ajudam a valorizar ainda mais o papel da estatística descritiva: ela não apenas resume os dados, mas também nos força a pensar criticamente sobre como interpretá-los.

Afinal, entender a realidade é muito mais do que apenas calcular números.

Medidas de dispersão

Até aqui, falamos sobre as medidas de tendência central, que nos ajudam a identificar um "ponto de equilíbrio" nos dados.

Mas, apenas saber onde está o centro não é suficiente para compreender completamente um conjunto de dados.

As medidas de dispersão mostram o quanto os dados estão espalhados ao redor desse ponto central.

Imagine que dois grupos de estudantes obtiveram, em média, a mesma nota em uma prova. Parece que os dois grupos tiveram desempenhos semelhantes, certo?

Porém, ao analisarmos as dispersões, podemos descobrir que no primeiro grupo as notas variam entre 8 e 10, enquanto no segundo grupo vão de 0 a 10. Nesse caso, a média sozinha não conta toda a história.

Amplitude

A amplitude é a distância entre o ponto mais baixo e o ponto mais alto de um conjunto de dados e fornece uma visão geral da dispersão dos dados.

Ela é calculada como Valor Máximo – Valor Mínimo.

Python

# Conjunto de notas
notas = [4, 8, 6, 10, 5]
# Amplitude
amplitude = max(notas) - min(notas)
print(f"Amplitude: {amplitude}")

R

# Conjunto de notas
notas <- c(4, 8, 6, 10, 5)
# Amplitude
amplitude <- max(notas) - min(notas)
print(paste("Amplitude:", amplitude))

Aqui, o maior valor é 10 e o menor é 4. Logo, o alcance é 6. Ele é simples de calcular, mas não nos diz nada sobre como os outros valores estão distribuídos.

Por exemplo, em [4, 4, 4, 10], o alcance também seria 6, embora o comportamento dos dados seja completamente diferente.

Já a variância e o desvio padrão são medidas mais robustas, que levam em conta a dispersão de todos os valores do conjunto em relação à média.

Variância

A variância nos informa quão distantes, em média, estão as notas de uma turma em relação à média da nota da turma.

O cálculo segue três etapas principais:

1. Calcula-se a média dos dados.
2. Para cada valor, calcula-se a diferença entre ele e a média, elevando essa diferença ao quadrado (para eliminar os sinais negativos e penalizar desvios maiores)
3. Soma-se esses valores e divide-se pelo número total de dados.

Essa soma dos quadrados das diferenças normalizadas dá a variância, que vai dizer o quão afastados da média estão os dados.

Python

import numpy as np
# Notas da turma
notas = [4, 8, 6, 10, 5]
# Variância
variancia = np.var(notas, ddof=0)  # ddof=0 para população
print(f"Variância (população): {variancia}")

R

# Conjunto de notas
notas <- c(4, 8, 6, 10, 5)
# Variância
variancia <- var(notas)  # Para amostras
print(paste("Variância (amostra):", variancia))

Na prática, valores altos de variância indicam dados mais dispersos, enquanto valores baixos indicam que os dados estão mais próximos da média.

Desvio Padrão

O desvio padrão é a raiz quadrada da variância e, por isso, tem a mesma unidade dos dados originais, o que facilita a interpretação.

Em vez de trabalhar com "quadrados de unidades", ele nos diz diretamente, em média, quanto cada valor se desvia da média.

Por exemplo, se as notas de uma turma têm um desvio padrão de 2, isso significa que, em média, as notas estão a uma distância de 2 pontos da média.

Python

# Desvio padrão
desvio_padrao = np.std(notas, ddof=0)  # ddof=0 para população
print(f"Desvio Padrão (população): {desvio_padrao}")

R

# Desvio padrão
desvio_padrao <- sd(notas)  # Para amostras
print(paste("Desvio Padrão (amostra):", desvio_padrao))

Assim como na variância, quanto menor o valor, mais “concentrados” e “uniformes” são os valores do conjunto de dados.

Resumindo

• A amplitude mostra quanto os dados se espalham, medindo a distância entre o menor e maior número;
• A variância reflete a dispersão em torno da média;
• O desvio padrão está na mesma unidade de medida dos dados iniciais e é a média de quanto os valores se distanciam da média.

Analisando o desvio padrão, amplitude, média e mediana em conjunto, por exemplo, é possível ter uma visão muito mais acurada do comportamento dos dados do que ao analisar uma única métrica!

Representações gráficas

Os gráficos permitem identificar padrões e características dos dados que podem não ser evidentes apenas pelos números.

Dois gráficos amplamente utilizados na estatística descritiva são o histograma e o boxplot.

Histograma

O histograma é um gráfico de barras de distribuição. Ele vai mostrar como os dados estão distribuídos em intervalos definidos.

No eixo y, veremos a quantidade de dados e, no eixo x, a faixa de valores de cada intervalo.

Ou seja: a altura de cada barra indica quantos dados cabem dentro de cada intervalo.

No exemplo abaixo, imagine uma situação de tempo de espera para clientes de um e-commerce.

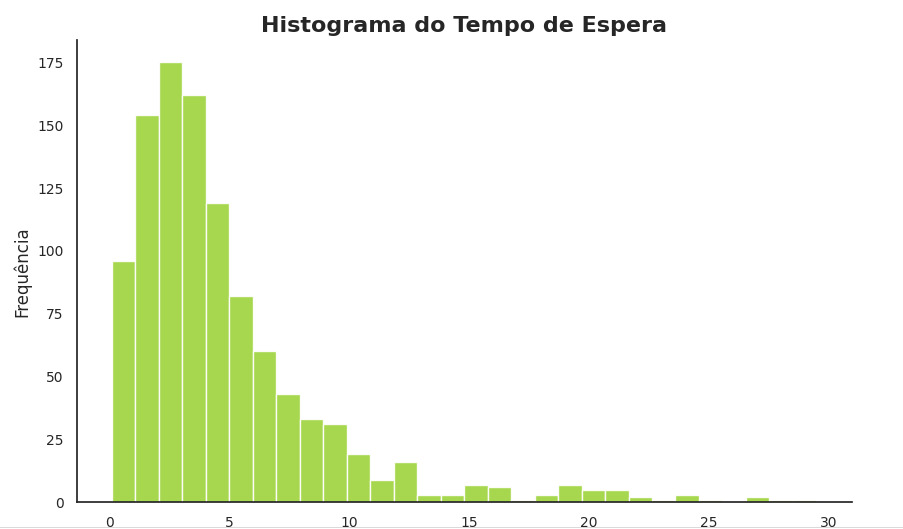
O que podemos observar no exemplo:

• A maior parte dos tempos de espera está concentrada nos intervalos mais baixos (entre 0 e 6 minutos). Isso indica que a maioria das pessoas esperou pouco tempo.
• A distribuição é assimétrica à direita, ou seja, há uma "cauda" se estendendo para valores maiores de tempo de espera, sugerindo a presença de alguns casos isolados com esperas mais longas.
• O histograma é útil para identificar padrões, como concentração de dados (moda), lacunas (intervalos sem dados) e tendências gerais.

Boxplot

O boxplot (ou gráfico de caixa) é uma representação visual que destaca a dispersão e os valores extremos.

Ele é baseado nos quartis, que são os pontos que dividem o conjunto de dados em 25%, 50% e 75%.

Como interpretar:

• A linha central na caixa representa a mediana. No exemplo, ela indica que 50% dos tempos de espera são menores do que esse valor.
• As bordas da caixa correspondem ao primeiro quartil (Q1) e ao terceiro quartil (Q3), delimitando o intervalo interquartil (IQR), onde estão os 50% centrais dos dados.
• Os "bigodes" se estendem até os menores e maiores valores que não são considerados outliers (valores dentro de 1,5 vezes o IQR).
• Os pontos além dos bigodes são outliers, ou seja, tempos de espera muito acima do esperado.

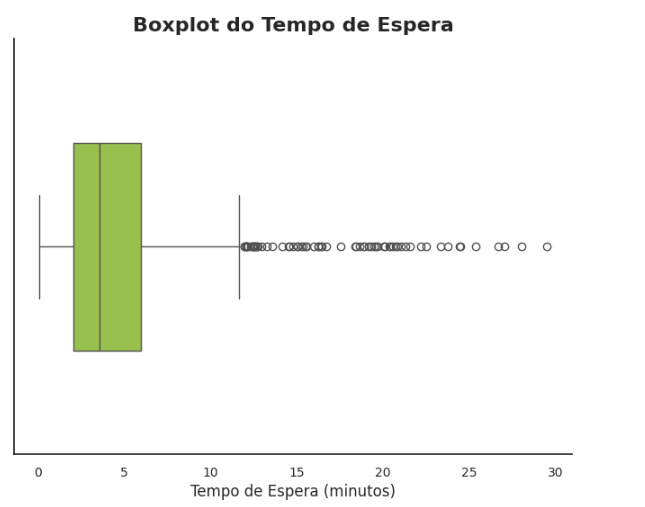
O que podemos observar no exemplo:

• A caixa está concentrada em tempos de espera baixos, confirmando que a maioria dos dados está próxima da mediana.
• Há vários pontos isolados à direita do gráfico, representando tempos de espera muito altos. Esses outliers podem indicar anomalias ou situações específicas, como falhas no processo ou casos atípicos.

Na estatística descritiva, esses gráficos são importantes pois ajudam a traduzir os números em representações visuais, tornando mais intuitivo para a pessoa analista entender as características dos dados.

Para se aprofundar no entendimento desses gráficos e conhecer outras possibilidades, indico a leitura do artigo Como escolher o tipo de visualização de dados para sua análise.

Conclusão

Ufa! Aprendemos bastante sobre a estatística descritiva. Lembre-se de sempre nutrir um olhar crítico e curioso em relação aos dados que você está analisando e também ao interpretar as estatísticas que te contam, por aí.

Afinal, os dados contam histórias, e cabe a nós interpretá-las com cuidado e responsabilidade.

Ao analisar questões complexas, como a saúde econômica de uma população, é imprescindível explorar todas as métricas e conhecer bem o comportamento dos dados.

Com IA, já é possível gerar a análise descritiva a partir de um pedido em texto e focar na interpretação.

Aqui na Alura, temos alguns cursos bem legais explorando a fundo todos os conceitos que vimos e colocando a mão na massa com situações do dia a dia de uma pessoa que lida com dados. Te vejo por lá!