Testes de hipótese: definição, utilidade e tipos principais
Já se perguntou como os cientistas conseguem determinar com tanta segurança se uma nova dieta realmente ajuda na perda de peso ou se um remédio alivia os sintomas de uma doença?
Essas respostas não vêm do acaso, mas de métodos rigorosos que avaliam suposições com base em dados e probabilidades.
É assim que os testes de hipóteses entram em cena: ferramentas essenciais para validar resultados e tomar decisões baseadas em evidências.
Mas você sabia que existem diferentes tipos de testes, cada um com suas próprias regras e aplicações? E como a escolha errada pode levar a conclusões equivocadas?
Neste artigo, vamos explorar o universo dos testes de hipóteses, entender os erros que podem surgir no processo e como utilizá-los corretamente. Preparado para desvendar o poder da análise estatística?
Vem comigo e vamos descobrir como esses testes transformam dados em conhecimento.
O que são testes de hipóteses e para que servem?
Imagine que você está investigando uma questão importante, como saber se um novo remédio realmente funciona, se duas características estão relacionadas ou se os resultados de um experimento seguem um padrão esperado.
Para responder a perguntas como essas, usamos uma ferramenta chamada teste de hipóteses.
Um teste de hipóteses é como um detetive: ele analisa os dados usando regras baseadas na probabilidade para decidir entre duas hipóteses:
- Hipótese nula (H₀): é a ideia inicial, que geralmente diz que "não há efeito", "não há diferença" ou "não há relação".
- Hipótese alternativa (H₁): é a hipótese oposta, que sugere que "há algo acontecendo", como uma diferença real ou uma associação.
Os testes estatísticos podem ser usados em várias situações, como:
- Comparar dois grupos, por exemplo, um grupo que tomou um remédio versus outro que não tomou, para ver se há uma diferença significativa.
- Verificar se duas coisas estão relacionadas, como o tempo de estudo e as notas em uma prova.
- Checar se os resultados seguem o padrão esperado, como os números de um dado sendo igualmente distribuídos.
No fim, o teste ajuda a responder: os dados que observamos são compatíveis com a hipótese nula, ou há evidências fortes o bastante para rejeitá-la e considerar a hipótese alternativa?
Assim, ele nos dá uma base para tomar decisões informadas em meio à incerteza.
Quando usamos testes estatísticos, queremos entender padrões nos dados, comparar grupos ou verificar relações entre variáveis.
Para isso, existem dois tipos principais de testes: paramétricos e não paramétricos. Vamos descobrir a diferença entre eles e os mais utilizados.

Tipos de testes de hipóteses
De forma geral, esses são os principais tipos de testes de hipóteses.
Paramétricos
Os testes paramétricos assumem que os dados seguem uma distribuição específica (geralmente normal) e possuem variâncias homogêneas.
Eles são mais poderosos quando essas suposições são atendidas, pois utilizam mais informações sobre os dados.
Principais testes paramétricos:
- Teste t de Student (para uma ou duas amostras): compara médias de uma ou duas populações.
- Hipótese nula (H₀): não há diferença entre as médias (μ1=μ2).
- Hipótese alternativa (H₁): as médias são diferentes (μ1≠μ2).
- Teste z: semelhante ao teste t, mas usado para grandes amostras (quantidade de elementos n>30) ou quando a variância populacional é conhecida.
- Hipótese nula (H₀): a média da amostra é igual à média da população (X=μ).
- Hipótese alternativa (H₁): a média da amostra é diferente da média da população (X≠μ).
- Teste qui-quadrado (χ2): avalia associações entre variáveis categóricas ou adequação de um modelo teórico.
- Hipótese nula (H₀): não há associação entre as variáveis.
- Hipótese alternativa (H₁): existe associação entre as variáveis.
- Teste F (ANOVA): compara médias de três ou mais grupos.
- Hipótese nula (H₀): as médias dos grupos são iguais.
- Hipótese alternativa (H₁): pelo menos uma média é diferente.
Não Paramétricos
Os testes não paramétricos não dependem de suposições rígidas sobre a distribuição dos dados.
Eles são mais versáteis e usados quando as condições dos testes paramétricos não são atendidas.
Principais testes não paramétricos:
- Teste de Mann-Whitney (ou U de Mann-Whitney): compara distribuições de dois grupos independentes.
- Hipótese nula (H₀): as distribuições dos dois grupos são iguais.
- Hipótese alternativa (H₁): as distribuições são diferentes.
- Teste de Wilcoxon (para amostras pareadas): compara dados pareados, como antes e depois de um tratamento.
- Hipótese nula (H₀): não há diferença nas medianas.
- Hipótese alternativa (H₁): há diferença nas medianas.
- Teste de Kruskal-Wallis: alternativa ao teste F (ANOVA) quando os dados não atendem às suposições paramétricas.
- Hipótese nula (H₀): as distribuições dos grupos são iguais.
- Hipótese alternativa (H₁): pelo menos um grupo tem distribuição diferente.
- Teste de Friedman: compara distribuições de três ou mais grupos relacionados.
- Hipótese nula (H₀): as distribuições são iguais.
- Hipótese alternativa (H₁): pelo menos uma distribuição é diferente.
Testes unicaudais e bicaudais
Além dos diferentes tipos, os testes de hipóteses podem ser classificados como unicaudais ou bicaudais, dependendo do tipo de diferença que você deseja verificar nos seus dados. Isso tem a ver com o que você espera encontrar no experimento.
- Teste unicaudal: verificar se os valores estão em uma direção específica (por exemplo, se um grupo é maior ou menor que o outro). Usamos testes unicaudais quando já temos uma ideia clara da direção da diferença antes de realizar o teste.
- Hipótese nula (H₀): não há diferença na direção esperada. Exemplo: μ1≤μ2 (o grupo 1 é menor ou igual ao grupo 2).
- Hipótese alternativa (H₁): existe uma diferença na direção esperada. Exemplo: μ1>μ2 (o grupo 1 é maior que o grupo 2).
- Teste bicaudal: verifica se há uma diferença em qualquer direção (ou seja, se um grupo é maior ou menor que o outro). Usamos testes bicaudais quando não sabemos antecipadamente em que direção a diferença pode ocorrer.
- Hipótese nula (H₀): não há diferença entre os grupos. Exemplo: μ1=μ2 (os dois grupos são iguais).
- Hipótese alternativa (H₁): existe diferença em qualquer direção. Exemplo: μ1≠μ2 (os grupos são diferentes).
Tipos de erro
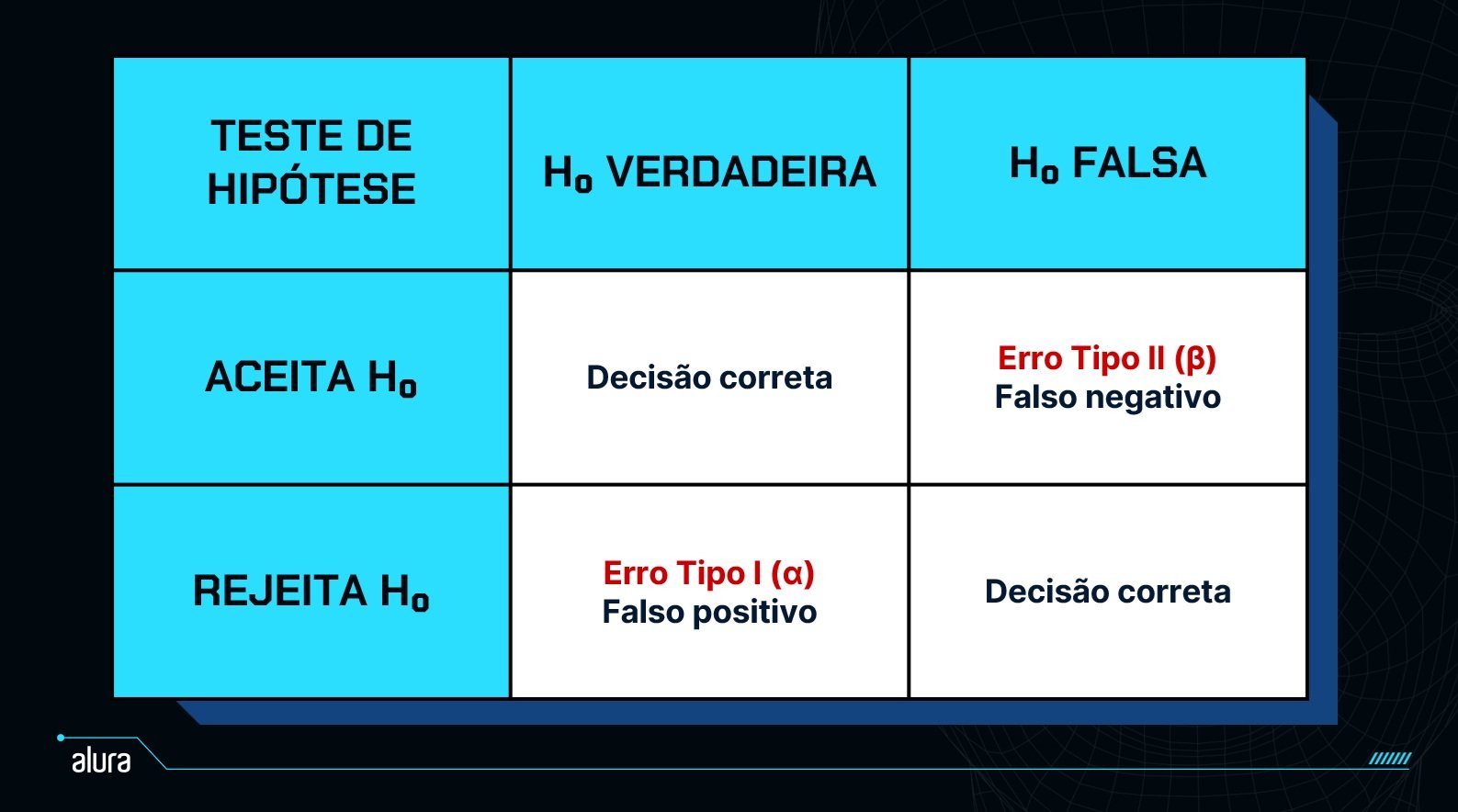
Em testes de hipóteses, há dois tipos principais de erros que podem ocorrer durante a análise de dados:
Erro Tipo I (α):
Esse erro acontece quando rejeitamos a hipótese nula (a suposição inicial) quando ela é verdadeira. Isso significa que, apesar da hipótese nula estar correta, nós concluímos que ela está errada.
Exemplo: Imagine que estamos testando um medicamento e concluímos que ele é eficaz, quando na verdade ele não é.
Esse tipo de erro está relacionado ao nível de significância (α), que é geralmente fixado em 5%. Ou seja, aceitamos um risco de 5% de cometer esse erro.
Erro Tipo II (β):
Esse erro ocorre quando não rejeitamos a hipótese nula quando ela é falsa. Ou seja, não conseguimos detectar algo que realmente é verdadeiro.
Exemplo: Aqui, podemos concluir que um medicamento não é eficaz, mesmo quando ele realmente é. Esse erro está relacionado ao poder do teste (1 − β), que é a chance de detectar a diferença real, caso ela exista. Idealmente, o poder do teste deve ser acima de 80%.
Equilíbrio entre α e β:
Se diminuirmos o valor de α (por exemplo, de 5% para 1%), o risco de cometer o Erro Tipo I diminui, mas isso pode aumentar o risco de cometer um Erro Tipo II. Para compensar, seria necessário usar uma amostra maior para aumentar a precisão do teste.
Em resumo, os erros Tipo I e Tipo II representam riscos diferentes em testes estatísticos, e é importante encontrar um equilíbrio entre eles para garantir que as conclusões sejam confiáveis.
Estatística de teste
A decisão sobre rejeitar ou não a hipótese nula de um teste estatístico baseia-se no cálculo de uma estatística de teste a partir da amostra de dados.
A fórmula utilizada para esse cálculo varia conforme o tipo de teste, sendo determinada pela natureza do problema e pelas características dos dados disponíveis.
O teste Z por exemplo, possui a estatística Z como uma medida usada para determinar o quão longe, em termos de desvios padrão, um valor da amostra está da média esperada sob a hipótese nula. A estatística de teste é definida conforme a fórmula:
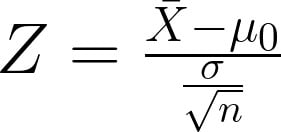 onde:
onde:
- X é a média da amostra.
- 𝜇0 é a média populacional ou o valor de referência sob a hipótese nula.
- 𝜎 é o desvio padrão populacional.
- 𝑛 é o tamanho da amostra.
Após o valor da estatística de teste ser calculado, ele é comparado a um valor crítico que depende do nível de significância do teste, que é o nível que controla o erro do Tipo I, ou seja, o risco de rejeitamos a hipótese nula quando ela é verdadeira.
Para um nível de significância de 5%, temos dois valores críticos em um teste bicaudal: -1.96 e 1,96.
Portanto, caso o valor de Z seja menor que -1.96 ou maior que 1.96, rejeitamos a hipótese nula em um teste bicaudal.
É possível visualizar esse exemplo a partir de um gráfico de distribuição normal, com média 0 e desvio padrão igual a 1.

O gráfico acima mostra a distribuição normal padrão, utilizada no teste Z. As áreas em vermelho representam as regiões críticas para um nível de significância de 𝛼=0.05 (teste bicaudal).
Os valores críticos são Z=−1.96 e Z=1.96. Se a estatística Z calculada cair em uma dessas áreas, rejeitamos a hipótese nula. Já a área verde no centro é a região de aceitação, onde não rejeitamos H₀.
Conclusão
Diante de tudo o que discutimos, é importante entender que os testes de hipóteses são fundamentais para garantir a precisão e a validade de qualquer análise baseada em dados.
A escolha entre testes paramétricos e não paramétricos pode ser decisiva para os resultados de uma pesquisa, dependendo das características dos dados e dos objetivos do estudo.
Se você deseja aprender ainda mais sobre estes testes e como podem ser utilizados na prática, confira os cursos que temos disponíveis sobre esse assunto:
Esses cursos são uma excelente oportunidade para transformar sua carreira e aplicar as melhores práticas em análises estatísticas para resolver problemas reais.











