Redes Neurais Convolucionais: Deep Learning com PyTorch

Conceitos Gerais - Apresentação

Olá e muito prazer eu me chamo Camila Laranjeira, esse aqui é o curso de Redes Neurais Convolucionais, antes de falarmos sobre o curso é importante mencionar que esse curso ele depende fortemente de conhecimentos que estão em outros dois cursos que é o de introdução a redes neurais e treinando uma rede neural.

Nesse curso principalmente o de introdução a redes neurais, vamos aprender os elementos essenciais de uma rede que é uma conexão o que que são camadas que são conhecimentos que vão ser assumidos como você já está familiarizado com eles, então é importante que você pelo menos tenha conhecimento base de redes neurais, então recomendo fortemente assistir os dois cursos que são uma introdução a esse.

Nesse curso de Redes Convolucionais vamos cobrir todo conhecer específico de uma Rede Convolucional. Como por exemplo, o que que é uma imagem como que olhamos para uma imagem de forma matemática, a representação base dela.

Vamos conhecer as diferentes representações de Redes Convolucionais para que vocês quando vejam uma rede representada em algum livro, em algum blog, você já entenda o que é cada elemento ali representado.

Vamos explicar o que é o “aprendizado Hierárquico” e por que no caso de Redes Convolucionais, é especialmente interessante você ter uma rede mais profunda, os benefícios disso, daí por diante nós vamos conhecer as principais aplicações da Rede Convolucional, explorando os datasets que o Torchvision provê, então vocês vão conhecer a ferramenta essencial que é o Torchvision que traz vários modelos prontos, vários conjuntos de dados prontos e ao melhor amigo de quem usa PyTorch para imagens .

Depois vamos conhecer a convolução desde a convulsão 1D, fazendo classificação de sinais 1D com a convolução, vai ser bem divertida essa prática. Vamos passar também pela convolução 2D que é efetivamente o que nós usamos para imagens, qual que é o comportamento de uma convulsão 2D.

Qual é a saída de cada filtro convolucional, o que é um filtro convolucional, como que ele interage com a imagem, vamos conhecer também a camada efetivamente do “PyTorch”, cada um dos parâmetros desta camada vocês vão se familiarizar com a importância desse parâmetro.

Vamos conhecer outras camadas como a camada de pulling e a camada de batch normalization, aqui no pulling vamos entender a segunda operação mais importante da convolução, vamos implementar tanto pulling quanto o batch normalization são essenciais para o treinamento de um bom modelo.

Implementaremos aqui esse bloco convolucional completo com todas as camadas, as mais importantes, todas que nós vamos aprender nesse curso, aí vamos chegar na parte que eu acho a mais interessante para quem decidiu fazer esse curso que é treinar uma CNN do zero.

Então aqui, faremos tudo do zero, desde a implementação na de uma arquitetura convolucional até o treinamento completo de uma rede. Esse conhecimento que está aqui do treinamento de uma rede, ele é todo esse curso aqui de Treinando uma rede neural Deep Learning com PyTorch, mas vamos tomar o cuidado de revisar esse conteúdo na hora de fazer o treinamento da rede convolucional.

E por fim para ser a cereja do bolo, nós vamos conhecer outras estratégias de treino usando uma rede convolucional como extrator de características e fazendo Fine-Tuning que é um dos usos mais comuns de um CNN.

[04:08 ] Então nós iremos aprender que no mundo de Redes Convolucionais no processamento de imagens é comum e recomendável que você aproveite conhecimento treinado em outros datasets, então você não precisa treinar o seu modelo do zero, não precisa se basear só no seu conjunto de dados na hora de treinar numa Rede Convolucional.

Você também pode aproveitar redes pré-prontas modelos pré treinados para que seu ponto de partida seja de uma rede já inteligente, uma rede já é treinada. Uma última recomendação é: faça os exercícios e usem o fórum, porque é interessante que vocês tenham certeza de que aprenderam e os exercícios foram pensados para você validar o seu aprendizado.

Eu tomei muito cuidado na criação dos exercícios, para que ele aborde parte do conteúdo que costumam ser os mais difíceis de aprender, então eu recomendo que vocês façam os exercícios .

[05:12 ] Vai ser um prazer estar aqui com vocês ao longo desse curso e eu espero que vocês aproveitem muito, bom aprendizado para você.

Conceitos Gerais - Motivação

Olá pessoal, vamos começar então a falar um pouco sobre Redes Neurais Convolucionais, começando a partir dos conceitos gerais que basicamente nós falaremos desde a motivação de porque se usa esse tipo de rede, até os elementos que compõem a arquitetura os principais, e terminando essa aula com os principais problemas que nós resolvemos com a convolução com a Rede Convolucional.

[00:28 ] Começando com motivação, vamos primeiro entender o que é uma imagem propriamente falando em termos computacionais, que nada mais é que uma matriz de pixels, são números organizados numa matriz.

Nesse caso, uma matriz quadrada de dimensões 256x256. que em outras palavras significa que são 246 números por 256 números, é uma matriz quadrada de números que nós vamos ver como isso se transforma numa imagem.

Então se nós pegarmos um trecho dessa imagem, o olho da Lena nós conseguimos ver nesse pedaço pequeno, os quadrados certos que são os pixels, que definem a imagem.

E em termos simples esses pixels, esses quadrados são a intensidade da cor daquele elemento, daquele quadrados. Então se eu tenho uma matriz, nesse caso 15 por 15, que a região do olho em um determinado elemento tem valor de 0.1, está perto de 0 então representa algo mais próximo do preto, 0.9 está mais perto do 1 representa algo próximo do branco e 0.5, 0.6 está na faixa dos cinza.

Vamos relembrar então o “Multilayer Perceptron” que nós já falamos aqui na Alura, no curso de introdução a Redes Neurais com PyTorch. Recomendo muito assistir, vai ser essencial para esse curso, e o Multilayer Perceptrons ele é a rede mais tradicional, a rede do Deep learn mais tradicional, e ele basicamente é composto por camadas de neurônios.

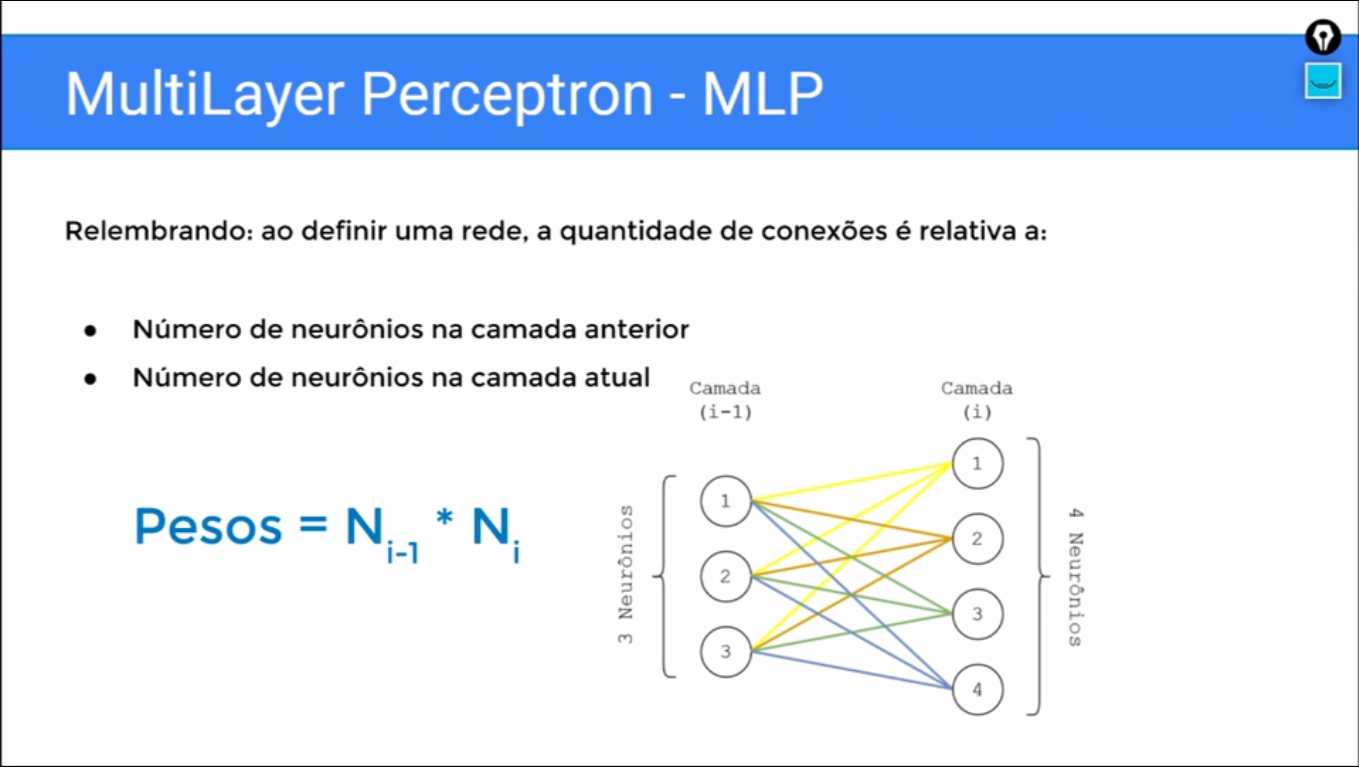
Camadas de uma dimensão vetores, de neurônios totalmente conectados, quando nós vamos definir o MLP a quantidade de conexões relativa ao número de neurônios da camada anterior e o número de neurônios da camada atual.

E o número de conexões, cada conexão lembrando é um peso vai ser dado pelo produto desses dois valores ´Pesos = Ni-1*Ni´que eu preciso conectar todo mundo com todo mundo, se eu tenho três neurônios de um lado, quatro neurônios do outro, eu vou ter 12 conexões ligando essas camadas.

No caso da nossa imagem da Lena que é 256 por 256, se nós fossemos tentar usar um MLP, nós temos na mão aqui essa imagem que é uma matriz quadrada, só que o MLP só aceita entradas 1D. Ele trabalha dessa forma, a arquitetura é feita dessa forma.

Então, nós teríamos que linearizar essa imagem ficando com n ao quadrado valores, tudo bem, nós linearizamos, nós conseguimos usar no MLP, só que aí vem uma outra questão, é quantos neurônios a próxima camada vai ter?

Cada problema vai ter a sua complexidade específica, mas em geral para você conseguir uma boa representação, a camada subsequente tem que ser diretamente proporcional ao tamanho da camada anterior, porque não faz muito sentido, eu ter n ao quadrado pixels que é 256 por 256 e a próxima camada eu ter 10 neurônios.

Vou perder muita informação, eu não vou conseguir aprender boas características dessa minha entrada.

Então eu teria que, por exemplo, ter uma camada subsequente igual 1 n ao quadrado Pixel, lógico que no mundo real não precisa ser igual, mas tem vezes que até maior do que o tamanho da entrada a camada.

Então se nós supormos uma situação intermediária, onde a camada subsequente é do tamanho da entrada, nós teríamos duas camadas de N ao quadrado pixels em uma camada e n ao quadrado neurônios na outra camada.

Para conectar essas coisas, teríamos um total de n à quarta conexões, cada conexão é um peso, então n a quarta peso, lembrando a nossa imagem tem 256 por 256, então que nós teria 236 a quarta pesos que são 4 bilhões de pesos que ocupa 17GB de memória.

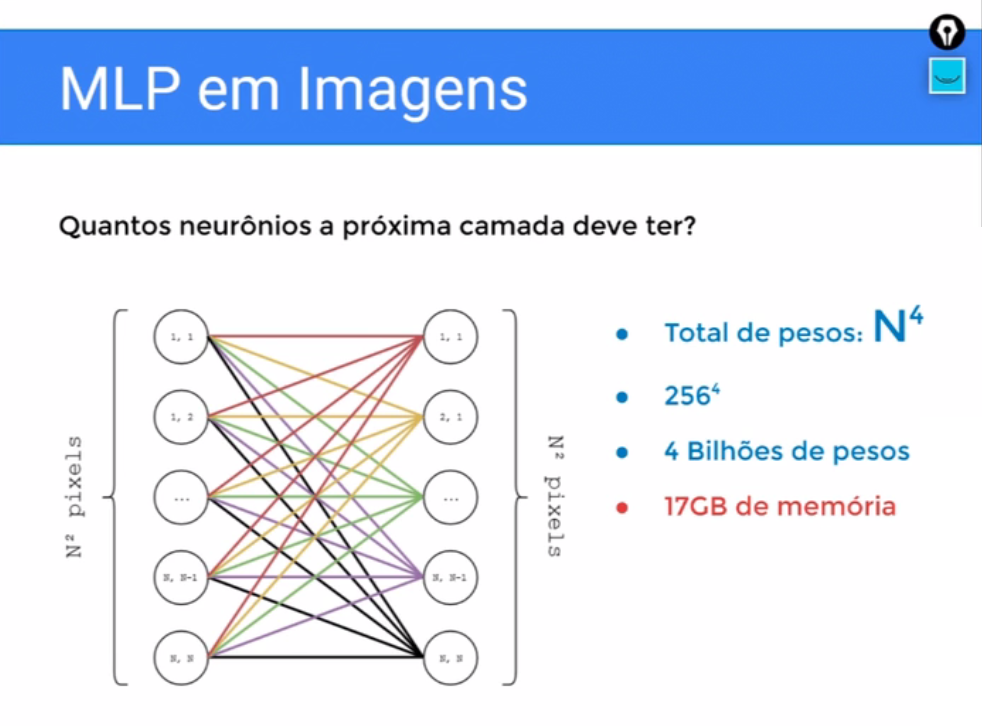
Só para você armazenar essa rede, nós não estamos falando de treinar, não estamos falando do gasto que você vai ter carregando coisas além da rede, só a rede são 17 GB de memória. Por isso, não usamos LMP para imagens, tem essa restrição, você teria que usar muitos parâmetros para conseguir uma boa representação.

Então daqui para frente vamos conhecer as Redes Neurais Convolucionais, que se baseia na operação da convolução, por isso que elas chamam convolucionais, em inglês Convolutional Neural Networks, então quando eu falar CNN eu tô falando das redes Neurais Convolucionais.

O número de parâmetros não vai ser mais vinculado ao tamanho da entrada, nós vamos conhecer o Kernel da convolução e o tamanho desse Kernel não depende do tamanho da entrada e resolve o problema de muitos parâmetros.

Por fim, uma coisa que se tornou essencial, inclusive para muitas aplicações, é que a Rede Convolucional interpreta a imagem de forma intuitiva.

Então nós vamos conhecer um pouco melhor, não tanto quanto eu gostaria, mas as características são apreendidas por essas redes, são algo que conseguimos interpretar visualmente, inclusive as Redes Convolucionais são as mais usadas quando se tenta produzir algum tipo de interpretabilidade da metodologia baseada em Deep learning, elas facilitaram nessa visualização.

Conceitos Gerais - Arquitetura da CNN

Agora nós vamos falar um pouco sobre Arquitetura da CNN, bom, relembrando mais uma vez o MLP,eu acho importante nós fazermos essas comparações para entender o papel da CNN e quando usá-la.

Ele recebe um vetor, nós já comentamos isso, um vetor de uma dimensão e as camadas são totalmente conectadas, ou seja, cada neurônio vai se conectar à todos os elementos da entrada, que foi o que comentamos agora pouco do problema de você ter uma dimensionalidade muito grande nas imagens e isso tem inviável para o uso no MLP.

As imagens, nós ainda nem comentamos de imagens coloridas. Elas são volumes. Então no caso das imagens das RGB que é vermelho, verde, azul. Elas são volumes de três canais: um canal azul, um canal verde, um canal vermelho e possuem altíssima dimensionalidade, porque só essa imagem da Lena 256 x 256, se nós considerarmos os três canais ainda, totalizam mais de 190.000 pixels que se nós fossemos colocar numa rede totalmente conectada, totalmente inviável.

A CNN e nós já vamos começar a nos familiarizar com a representação, ela é apta a trabalhar com volumes 3D. Então nós vamos ver da CNN, sempre uma representação com profundidade também.

Então não só ela consegue trabalhar com matrizes, que são as matrizes quadradas ou não, como também ela lida com a questão da profundidade, nós vamos ver em breve como ela faz isso.

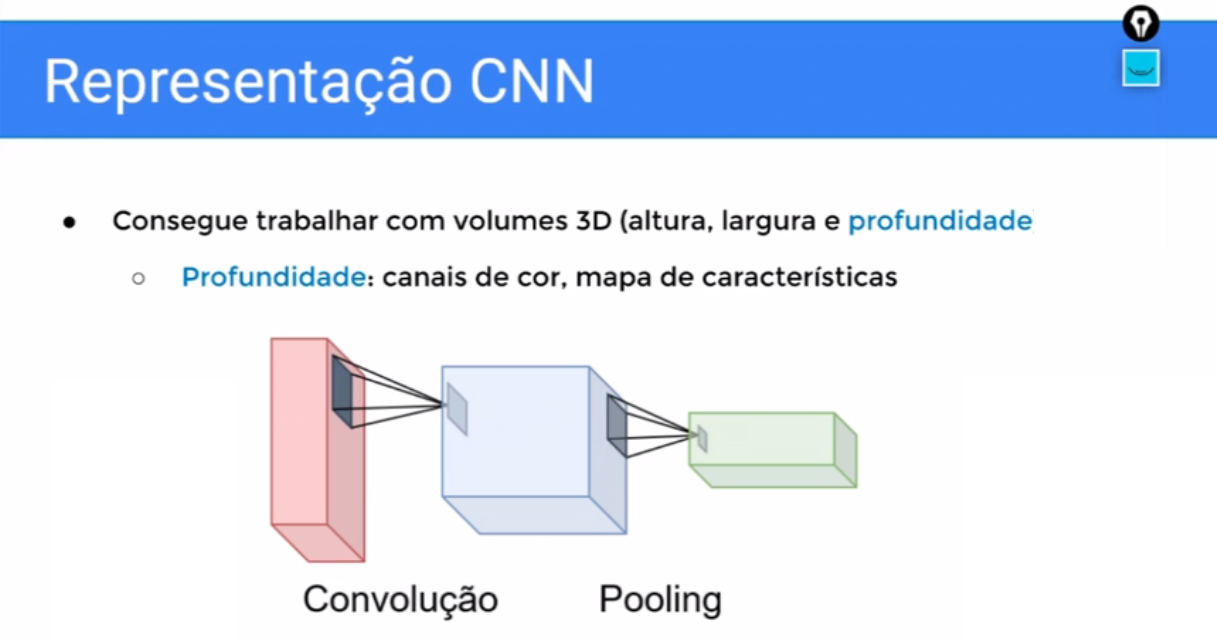
Essa profundidade quando nós estamos falando da entrada que aqui esse primeiro cubo seria a imagem, a partir da segunda camada, esses cubos são mapas de características; Lembrando que Redes Neurais Profundas, elas vão transformar a imagem em características isso é verdade para qualquer rede.

Então se nós transformarmos uma imagem a partir de uma camada de Rede Convolucional o que ela passa a ser é um mapa de características, também em três dimensões, só que aqui não estamos mais falando de canal de cor, estamos falando de mapa de características.

E os neurônios também são organizados em 3D e possuem um campo de visão limitado, então aqui nós estamos vendo as duas principais operações de uma CNN, que a convolução e o pooling

Então a convolução vai transformar a imagem em características e o Pooling é um processo “sub-amostragem” que nós vamos conhecer melhor, então a CNN vai justamente ficar alternando entre “transformação” e “subamostragem’, até o final.

Uma outra representação que podemos usar, também é uma representação em três dimensões, então só que dessa forma em vez de nós desenharmos cubos, desenhamos como se fossem as lâminas da representação, então é como se em vez de fazer esse cubo, eu separasse cada mapa de características, então aqui eu transformaria uma entrada que nesse caso eu fiz ela só com um canal em seis mapas de características através da convolução.

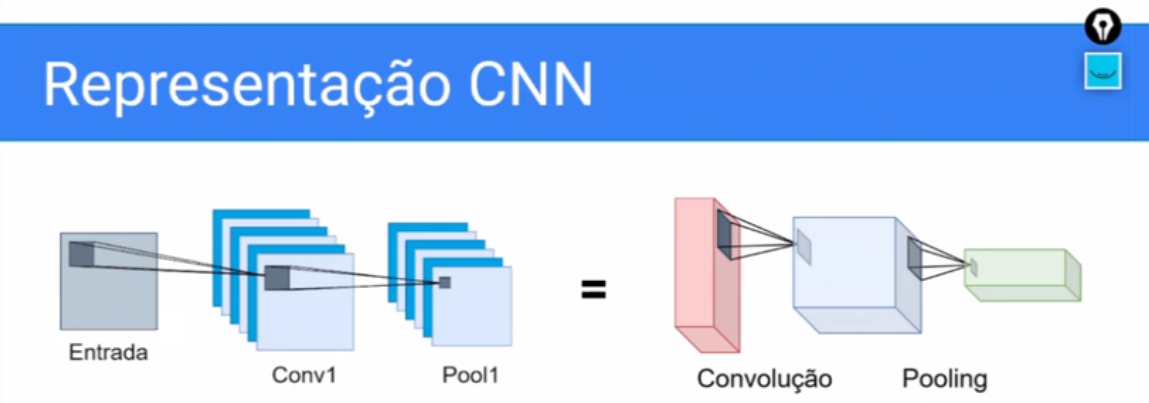
E quando nós compomos uma rede completa do começo até o final a tendência, que nós vamos entender melhor porque, é que quanto mais profunda a rede mais mapas de características a representação vai ter.

Então aqui nós passamos de seis mapas de características, para eu suponho que é 12, para o que eu suponho que é 18. Mas eu não lembro quando eu fiz esse desenho.

Então nós estamos alternando entre “transformação” e “subamostragem’, usando um filtro que tem um campo de visão limitado que nós vamos ver direito mais para frente como funciona.

Então alterna entre “transformação” e “subamostragem” e as camadas mais comuns são a Convolucional, que nós já falamos diversas vezes de transformação.

O pulling que a “subamostragem” e camadas totalmente conectadas que são essas aqui, azuis do final, que nada mais são do que as camadas que nós vamos usar para fazer uma inferência, por exemplo uma classificação, uma regressão, nós usamos camadas tradicionais totalmente conectadas, só que vão operar em cima de um conjunto de características em Alta Dimensão, nós vamos ver mais para frente o que que significa.

Vão operar com características melhores do que a imagem original. E essa forma de você compor a Rede Convolucional, produz um aprendizado hierárquico, por quê? Porque existe uma hierarquia de processamento, primeiro você passa na primeira camada, depois você passa na segunda, depois você passa na terceira,

Então aprendizado hierárquico, aprende uma característica em cima dessa característica você aprende outra e daí por diante. Então as primeiras camadas, como elas acessam diretamente a imagem, mais diretamente, elas vão aprender características de baixo nível, enquanto as últimas camadas vão aprender características de alto nível.

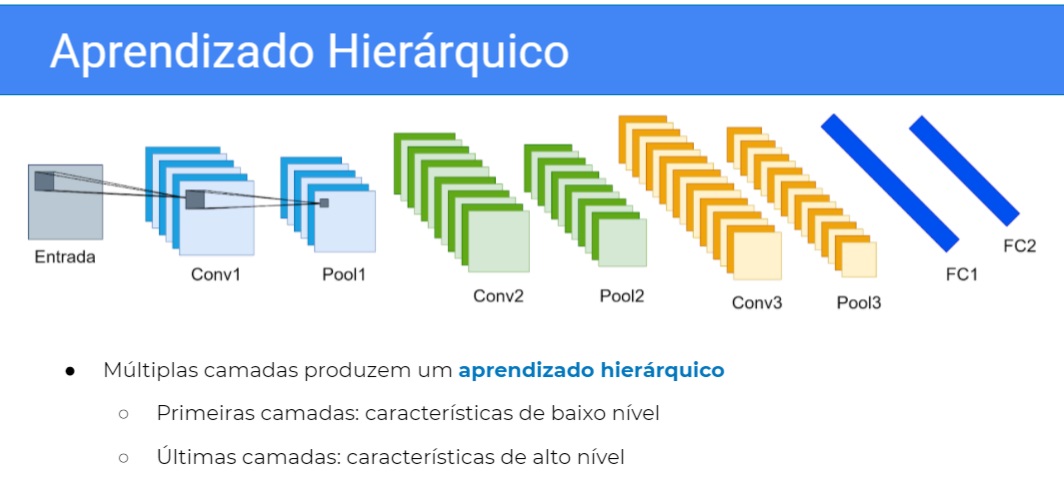
Então basicamente teríamos que pensar que essa entrada aqui é um objeto, acho que esse bicho aqui é um ganso, então vamos supor que é um. Aqui nós aprenderíamos nas primeiras camadas retas, quinas, blobs de cor, na camada intermediária nós aprenderíamos coisas de mais alta frequência, algo que talvez pudesse parecer um olho aqui embaixo.

E nas últimas camadas nós aprenderíamos formas mesmo, tipo a cabeça de um cisne ou ganso talvez, uma colmeia de abelhas, enfim aprenderíamos formas mais próximas dos objetos que nós conhecemos do mundo real.

Então essa hierarquia de características que é desde o baixo nível, até o médio e até o alto. Mais cedo na rede nós aprendemos só retas por exemplo, no nível intermediário nós aprendemos os olhos de um animal por exemplo, e no alto nível nós aprendemos a cabeça inteira do animal, digamos assim.

Essas imagens que nós estamos vendo aqui, são filtros reais, são camadas de pesos mesmo real da rede, vamos ver mais para frente e maiores detalhes mas é como se essas camadas estivessem buscando esse tipo de padrão. Então as camadas iniciais procurariam por retas, e as finais procurariam pela cabeça do cisne efetivamente.

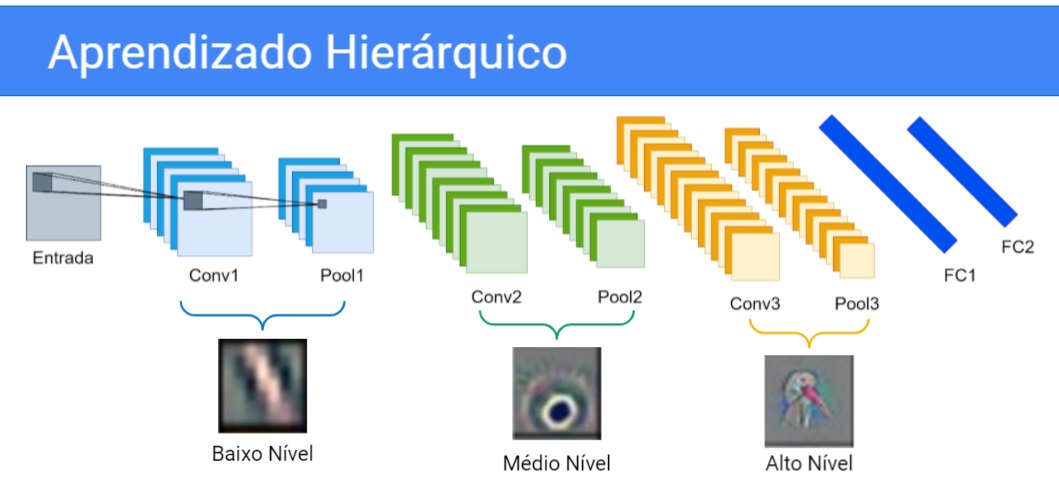
Então é isso, esse aprendizado que você tem que tirar dessa aula de que a CNN vai transformar hierarquicamente a imagem em características de cada vez mais alto nível e só no final vão fazer a inferência, que é a classificação a regressão em cima de características de alto nível.

Sobre o curso Redes Neurais Convolucionais: Deep Learning com PyTorch

O curso Redes Neurais Convolucionais: Deep Learning com PyTorch possui 242 minutos de vídeos, em um total de 53 atividades. Gostou? Conheça nossos outros cursos de Machine Learning em Data Science, ou leia nossos artigos de Data Science.

Matricule-se e comece a estudar com a gente hoje! Conheça outros tópicos abordados durante o curso:

• Conceitos Gerais
• Convolução 1D
• Convolução 2D
• Camada Convolucional no PyTorch
• Outras camadas no PyTorch
• Estratégias de Treino