Data Analysis: estatística com Google Sheets
Probabilidade - Apresentação
Olá, seja muito bem vindo ao nosso curso de Data Analysis, estatísticas com Google Sheets. O meu nome é Daniel Siqueira, eu vou ser seu instrutor nesse curso que, na realidade, já é continuação de outros dois cursos que temos na plataforma sobre análises de dados com Google Sheets.
Nesse curso ampliaremos ainda mais a base estatística para que consigamos fazer análises mais refinadas e mais rebuscadas. Começaremos aprendendo sobre probabilidade, os conceitos que envolvem probabilidade como, por exemplo, o espaço amostral, número de eventos, e desde o começo do curso faremos análises práticas com esses conceitos.
Depois aprofundaremos na probabilidade, veremos diversas formas de calcular probabilidade, dos conceitos mais clássicos para até os mais modernos, por exemplo, acusando a frequência relativa.
Entenderemos quando envolvemos incerteza, qual o melhor caminho para se tomar, como fazemos esse cálculo.
E depois que construirmos esse conceito juntos traremos situações práticas, situações clássicas como, por exemplo, o dilema das portas, essa é uma aula muito interessante em que você vai entender o tipo de raciocínio que podemos desenvolver usando a probabilidade para que você consiga fazer uma ponte para situações práticas no seu dia a dia, seja na sua empresa, seja nas suas análises.
Você vai conseguir entender esse raciocínio e isso vai te agregar bastante. Também aprenderemos a trabalhar com a probabilidade usando múltiplos eventos, por exemplo, quando eu tenho que fazer uma senha, qual a diferença de usar só letra, usar letra e número, outros símbolos, como fazemos esses cálculos misturando os conceitos da probabilidade.
Depois que construirmos toda essa base, chegaremos na parte que talvez seja a aplicação mais importante da probabilidade, que é o pay off ou, valor esperado.
Com esse conhecimento vamos conseguir fazer tomadas de decisões muito importantes como, por exemplo, quando vale a pena contratar um seguro ou não? Quando vale a pena investir em uma garantia estendida em um produto que eu comprei na loja?
Até também, fazendo uma ponte, para situações de tomadas de decisões da empresa, quando vale a pena para a minha empresa investir em um determinado produto ou em uma determinada estratégia, ou não. É um conhecimento muito importante e muito legal que vamos adquirir aqui no curso também.
Depois aprofundaremos sobre os conceitos estatísticos, sobre moda, olha só. Como calculamos moda, se tem uma função no Google Sheets, se não tem. A média e a mediana, qual a diferença entre ela, quando eu vou usar uma medida de tendência central ou não.
Também vamos aprender a resumir os dados através do Quartil, que é uma ferramenta muito útil e faremos uma análise bem legal utilizando o Quartil, misturando um pouco de data visualization, utilizando cores, construindo uma tabela e entenderemos quando é legal usar essa estratégia para resumir os dados.
Iremos aprofundar sobre os diferentes tipo de média, já trabalhamos com a média aritmética até agora, entenderemos que existem outros tipos e para cada situação de análise talvez seja melhor usar um tipo diferente de média. Aprenderemos sobre a média ponderada, sobre a média geométrica e as funções no Google Sheets.
Faremos uma análise também usando a média geométrica, por que existe a diferença da média aritmética e da média geométrica. E também veremos sobre a média harmônica.
Depois que construirmos todos esses conceitos, trabalharemos com Churn Rate, que nada mais é do que o total de clientes cancelados, faremos algumas análises usando o Churn. Olha só, o Churn absoluto, o Churn em porcentagem.
Aprenderemos como fazer uma análise de Cohort, tão falado hoje em dia, tão importante esse conhecimento para um analista de dados, faremos uma análise bem legal utilizando os gráficos, fazendo uma leitura bem completa para, no final, começarmos a responder perguntas muito práticas e muito interessantes.
Como, por exemplo, qual seria o tipo médio que um cliente entra no e-commerce e ele permanece como cliente? Bom, com um conjunto de dados, com essas análises de Churn Cohort eu consigo responder essas perguntas? Veremos que sim.
Fique conosco até o final, façam todas as atividades, eu tenho certeza que esse curso te dará uma base muito boa, muito sólida para que você consiga fazer mergulhos cada vez mais profundos.
Conte comigo no fórum de dúvidas, eu estou sempre lá para responder vocês, para apoiar vocês e nos vemos no próximo vídeo. Até lá.
Probabilidade - Espaço amostral
Observação: No slide, o instrutor apresenta, na verdade, o número de elementos do Espaço Amostral (n(S)), que é importante para o cálculo de probabilidades. Entretanto, podemos definir o Espaço Amostral como o conjunto de todos os resultados possíveis em um determinado experimento. Por exemplo, se jogamos um dado o nosso espaço amostral seria S = { 1, 2, 3, 4, 5 , 6 }, pois seriam esses os resultados possíveis nesse experimento.
Agora você foi convidado para participar de um grupo de analistas dentro do e-commerce do Clube dos Livros e esse grupo vai fazer uma série de análises envolvendo probabilidade, para isso você vai precisar fundamentar bastante os seus conhecimentos sobre esse tema.
Para começar, a sua colega pediu para você extrair de alguns dados que vocês têm de uma promoção que foi feita, você comprava um livro de determinado autor e você concorria a uma coleção de livros completa dele, temos alguns dados.
Sua colega te pediu para separar o espaço amostral e o número de eventos. Será que só com esses dados do sexo dos participantes, masculino e feminino, você consegue extrair o espaço amostral e o número de eventos? Vamos ver isso agora.
Toda vez que formos estudar probabilidade esses dois conceitos são muito importantes, espaço amostral e número de eventos.
O que é probabilidade? Probabilidade é o estudo de eventos e resultados envolvendo um elemento de incerteza, sempre quando eu tenho algum elemento de incerteza no ar, eu terei uma probabilidade associada, por exemplo, investir no mercado de ações, tem muita incerteza, eu sempre terei elementos de probabilidade associados.
Se eu fizer um lançamento, por exemplo, de uma moeda. Eu tenho como afirmar com certeza antes de jogar se vai dar cara ou coroa? Não, e nem você, ninguém pode.
Mas se, por exemplo, eu fizer 4 lançamentos seguidos da moeda, eu tenho como falar até de uma forma intuitiva que alguns resultados são mais fáceis de se obter, por exemplo, mais prováveis de se obter, do que outros.
É mais fácil, de repente, eu obter meio a meio, duas caras e duas coroas, do que de repente eu conseguir só 4 coroas seguidas. Já temos essa intuição de que, por exemplo, 4 resultados iguais é mais difícil.
Esse tipo de intuição, esse tipo de conhecimento é fundamental dentro das análises de dados e das tomadas de decisões, veremos como isso funciona.
Para conceituarmos melhor esse conhecimento da probabilidade vamos começar entendendo o que é o espaço amostral. O espaço amostral comumente é representado pela letra S, mas você pensa "Espaço amostral S?". É porque esse S vem de space, um termo em inglês.
Aliás, as ciências como um todo, as exatas, Física, comumente também tomam expressões, letras que vem de palavras em Inglês por ser uma linguagem universal. Quando você estiver estudando ou de repente encontrar alguma literatura e ver o espaço amostral com a letra S você já sabe que vem de space.
O espaço amostral, na verdade, é o conjunto de todos os possíveis resultados de um experimento aleatório, é a soma de tudo, por exemplo, vamos pensar em um lançamento de dados. Quais são as possíveis opções que eu tenho quando jogo um dado?
Um dado tem 6 faces, cada uma tem um número, eu posso tirar qualquer número dentro das 6 faces, meu espaço amostral é igual a 6 porque eu tenho a face número 1, a face numero 2, a face numero 3 e assim por diante. O espaço amostral é a soma de todos os possíveis resultados que eu tenho.
Já o evento é um subconjunto do nosso espaço amostral, geralmente ele é representado com uma letra maiúscula, como está na tela A, B, C. Se eu vejo uma letra maiúscula eu já sei que eu estou falando, mais ou menos, de um evento.
Para cada evento sempre tem uma probabilidade associada. Vamos entender um pouco melhor, pensando no lançamento de dados. Qual o número de eventos do dado cair com uma face par para cima?
Face par, vai até 6, temos as opções 2, 4 e 6, esses são os meus eventos. Repare que ele é um subconjunto do meu espaço amostral, ele pertence ao meu espaço amostral.
E o número de eventos do dado cair com uma face menor que 5? As opções que eu tenho são 1, 2, 3 e 4. Eu nunca vou ter um evento, por exemplo, que está fora do meu espaço amostral, eu não posso ter um evento na jogada de um dado, por exemplo, e obter 8, não dá, o meu evento sempre está fazendo parte do meu espaço amostral.
O que seria um evento impossível? Evento impossível, como o próprio nome já fala, é um evento que está totalmente fora do meu espaço amostral, como eu falei, tirar uma face 7 em um dado de 6 faces, não tem como logo, é um evento impossível.
Eu estou trazendo essas nomenclaturas para você porque no seu dia a dia quando alguém falar de forma técnica, você já sabe que evento impossível é quando ele está fora do espaço amostral.
Um evento certo é o oposto. Vamos pensar no Natal, qual é a probabilidade do Natal cair fora do dia 25 de dezembro? Nenhuma, todo ano cai no dia 25 de dezembro, é um evento certo e determinado.
E os eventos mutuamente exclusivos, o que são eles? É quando a presença de um impede o acontecimento do outro. Vamos pensar no lançamento de uma moeda, por exemplo, tem uma moeda diferente na tela.
Mas se eu jogo uma moeda e obtenho cara, ele já exclui a possibilidade de obter coroa, não dá para obter cara e coroa ao mesmo tempo, esses eventos são mutuamente exclusivos.
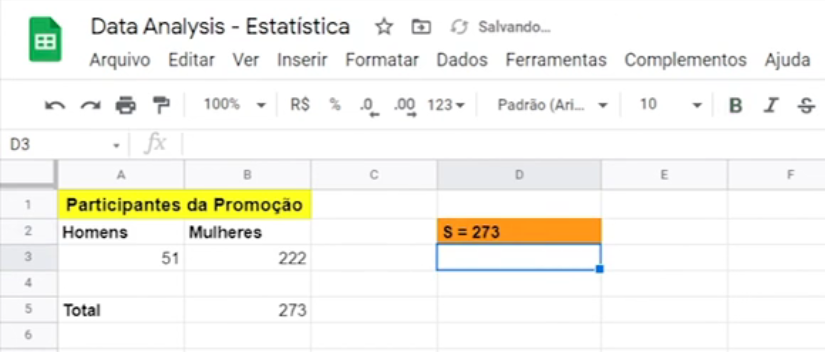
Vamos voltar para a nossa análise, agora que já entendemos o que é o espaço amostral, vamos pensar. Eu tenho o número de participantes, 51 homens e 222 mulheres, o meu espaço amostral vai ser a soma de todo mundo que eu tenho para fazer a minha análise, vai ser a minha própria frequência absoluta.
Para isso, eu vou colocar um total, eu vou copiar a formatação "Ctrl + C > Ctrl + Alt + V" para copiar só a formatação e vou escrever Total. Vamos dar um zoom para enxergarmos um pouco melhor.
Eu vou usar a nossa função soma "Digita SOMA", e vou somar quem? O meu total de homens e mulheres, fecho e dou Enter. Esse é o nosso espaço amostral, é igual a 273. Só para chamar mais atenção, eu vou colocar S = 273. Eu ainda vou pintar ele de laranja para dar um destaque maior. Esse é o nosso espaço amostral.
Probabilidade - Probabilidade
Agora que você já tem esses conhecimentos dos conceitos de espaço amostral e número de eventos, será que você consegue calcular probabilidade?
Sim, com certeza. Temos alguns caminhos, alguns conceitos para calcularmos probabilidade, vamos começar pelo conceito clássico.
Eu quero saber qual é a probabilidade nessa promoção de um sorteado ser do sexo masculino, ser um homem. Como fazemos? Vamos organizar "Participantes da Promoção > Ctrl + C > Ctrl + Alt + V" e vou colocar Probabilidade de ser homem.
Como calcularemos essa probabilidade pelo conceito clássico? Faremos a seguinte conta, vou dar um igual (=) para ele receber o cálculo e vou pegar o número de eventos que eu tenho, dentro das minhas opções quais são os eventos de ser homem? 51.
E eu vou dividir pelo meu espaço amostral que é o total de opções que eu tenho. E "Enter". Está aqui a probabilidade, “0.1868131868”
Sempre usamos probabilidade como porcentagem, fica um pouco mais fácil de visualizar, vou selecionar a célula, venho em Porcentagem, clico e está aí. A probabilidade de um sorteado ser homem é igual a 18,68%.
Por analogia eu consigo fazer a mesma coisa para as mulheres. Eu vou copiar aqui "Ctrl + C > Ctrl + Alt + V > Escreve Probabilidade de ser Mulher".
Qual é o número de eventos que eu tenho para as mulheres? 222. Vou dar um igual =B3, número de eventos que eu tenho dividido pelo meu espaço amostral, que são todas as possíveis opções que eu tenho aqui, /B5. "Enter". E aqui está, 0,8131868132. Vou transformar em porcentagem também. A probabilidade de ser mulher é 81%, ou seja, muito maior.
Esse tipo de cálculo que fizemos é o conceito clássico de probabilidade. Vamos entender um pouco melhor como funciona. Clássico ou a priori, você vai encontrar essas duas nomenclaturas. Ele foi feito por Laplace lá em 1812.
E ele sistematizou, ele começou a observar e estudar os jogos de cassinos, de cartas e de dados. Basicamente, esse conceito nos fala que eu tenho um experimento aleatório e eu tenho um espaço amostral, nós já entendemos que é o número de eventos. Experimentos e espaço amostral.
Para calcular a probabilidade desse evento eu vou pegar o número de eventos que eu tenho dividido pelo todo, pelo meu espaço amostral.
Dentro desse conceito tem algumas pressuposições básicas. Primeiro, o espaço amostral é sempre numerável e finito, eu não tenho um espaço amostral infinito, que eu não consiga contar e numerar. Os resultados do meu espaço amostral são equiprováveis, eles não podem ser impossíveis.
Eu também tenho outra forma de determinar a probabilidade através da frequência relativa. Vamos abaixar um pouco a tela, você vai ter a seguinte tabela para você fazer essa análise junto comigo. Deixa eu dar um duplo clique para ajustar.
Eu quero analisar agora a probabilidade dentro dos dados que eu tenho do comprador desse livro ter idade igual a 30 anos. Eu obtive esses dados dos compradores e eles estão aqui.
Vamos observar, minha primeira venda foi exatamente igual a 30, o número de ocorrências até aqui era 1, de 30 eu tinha 1 venda e 1 ocorrência, e minha frequência relativa era 1 por 1. Eu tinha um evento e ele já tinha alcançado o que eu queria, 1 de 1.
Depois, na segunda venda, a idade do comprador era de 19 anos, comprador ou compradora, eu continuei só com uma ocorrência, percebe que Ocorrências eu não alterei porque não é 30. E minha Frequência relativa ainda era 1 em duas compras.
Terceira, idade era 21 anos, não alterei minha Ocorrência, só tinha uma ocorrência com 30 anos, minha Frequência relativa era 1 em 3. E assim foi. Na quarta, 30 anos de novo, eu mudo o meu número de ocorrências, já tenho duas ocorrências com 30 anos, duas Frequências de quatro.
Eu posso fazer isso exaustivamente. O resultado que eu obtiver aqui, quanto maior for esse número de dados que eu tenho para analisar, ele vai se aproximando muito da minha probabilidade, só com a Frequência eu já consigo ter a noção muito próxima dessa minha probabilidade.
Esse conceito, esse modo de calcular é conhecido como o Conceito da Frequência relativa ou posteriori, ele foi desenvolvido pelo físico alemão Richard Von Mises.
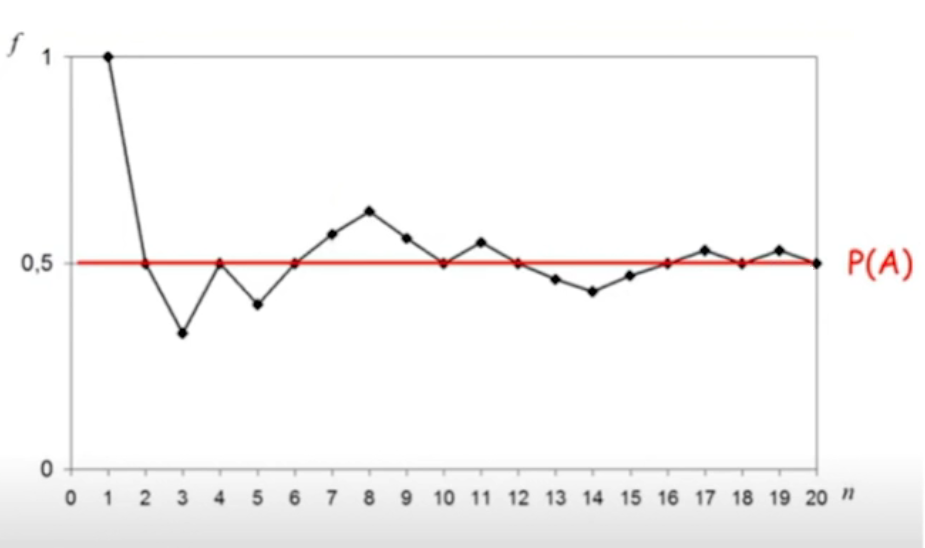
E conseguimos, na verdade, fazer uma estimativa da probabilidade analisando o número de repetições da frequência, quanto mais dados eu tiver ali, mais próxima essa minha probabilidade vai estar. Como calculamos isso?
Matematicamente a fórmula envolve limite, mas traduzindo a fórmula que é limite do n indo até o infinito com as frequências dos eventos que eu tenho. Lembra que eu falei que os eventos estavam com uma letra maiúscula? Aqui ele colocou como A.
É isso que acontece: eu tenho as minhas frequências e conforme eu vou aumentando os meus dados a minha leitura tende a alcançar a minha probabilidade.
Por fim, temos o Conceito Moderno ou axiomático. Ele tem esse nome porque ele se trata de axiomas, de condições para conseguirmos calcular probabilidade.
Vamos entender, só para você ter uma noção, tanto o conceito clássico, a priori, quanto o a posteriori, estão inclusos dentro do nosso Conceito Moderno, axiomático porque são os axiomas, são as condições para conseguirmos calcular probabilidade.
O primeiro conceito que temos é que a nossa probabilidade vai estar entre 0 e 1 “0 = <P(A) = < 1”. Traduzindo isso para porcentagem quer dizer que ela vai ser entre 0 e 100%, uma probabilidade não tem como ser maior do que 100%, faz todo sentido.
O nosso espaço amostral sempre é igual a 100%, “P(S) = 1” aqui está como 1, a probabilidade de ter o espaço amostral é 100% porque ele está envolvendo todas as nossas opções.
E tem um terceiro ponto que é muito importante, “P(A U B) = P(A) + P(B)” se A e B são eventos de S, meu espaço amostral, e são mutuamente exclusivos, ou seja, eu não consigo ter os dois ao mesmo tempo, a soma, a união da probabilidade de A e B é igual como se eu tivesse somando essa probabilidade de forma separada, eu posso calcular a probabilidade A separadamente e somar com a probabilidade de B.
Tanto faz eu unir todo mundo antes e calcular probabilidade e calcular só a de A e depois somar só a de B. Isso traz implicações muito importantes. Vamos analisar uma situação, um exemplo que eu trouxe.
Vamos supor que você esteja assistindo uma corrida, está todo mundo em cima do muro assistindo, uma corrida de sacos, a pessoa entra no saco e vai pulando. Eu tenho algumas informações, olha só.
Eu sei que a pessoa X é duas vezes mais provável de ganhar do que a pessoa Y. Eu tenho 3 pessoas, X, Y e Z. A primeira informação é que a pessoa X é duas vezes mais provável de ganhar do que a pessoa Y.
A pessoa Y é duas vezes mais provável de ganhar do que a pessoa Z. Qual a probabilidade de que Y ou Z ganhe?
Se você quiser, você pode dar uma pausada nessa tela agora e ler com um pouco mais de calma para tentar separar as informações. Meu espaço amostral é S= X ganha, Y ganha ou Z ganha.
Eu tenho alguma outra opção? Eu só tenho um ganhador logo, todos são mutuamente exclusivos. Todas as possibilidades que eu tenho estão ganha, X ganha, ou Z ganha, ou Y ganha.
E eu coloquei matematicamente o que falou no enunciado lá atrás, eu sei que a pessoa X é duas vezes mais provável de ganhar do que a pessoa Y.
A pessoa X é duas vezes, probabilidade de X é igual a duas vezes a probabilidade de Y. E a probabilidade de Y é igual a duas vezes a probabilidade de Z. Está aqui de novo na tela “P(X) = 2.P(Y) e P(Y) = 2.P(Z)”.
Eu sei que, olha só o axioma que acabamos de ver, “P(X) + P(Y) + P(Z) = 1” a probabilidade de X mais a probabilidade de Y mais a probabilidade de Z é igual a 1, ou seja, 100%. A soma das probabilidades é igual ao total que eu tenho no meu espaço amostral.
Como eu posso chamar, de repente, a probabilidade do meu Z de P, e eu sei que meu Y é duas vezes o P, o meu P(X) é duas vezes o Y, ou seja, quatro vezes o P.
Eu transformei todo mundo em uma letra, eu fiz uma troca, matematicamente usamos muito essa estratégia. E fazendo as contas, eu vou somar “4p + 2p + 1p = 7p”. O 7 está multiplicando, passa para lá dividindo.
A minha probabilidade é p=1/7. Agora eu consigo trocar o meu P era igual o do Z, 1/7, no Y eu sei que era o dobro do Y então é 2/7, e o X era o dobro do Y, igual a 4/7. Se eu somar todo mundo vai dar 7/7, que é igual a 1 inteiro. A probabilidade, que ele me perguntou, de Y união Z, porque era um ou o outro ganhar, eu posso somar as probabilidades, “2/7 + 1/7”.
Está aqui, 3/7, eu faço a conta, “P(Y U Z) = 3/7 = 0,4285 = 42,85%” vou achar meu resultado próximo de 0,42, transformando em porcentagem, 42,85%. Matematicamente eu consegui calcular a probabilidade com os nossos axiomas, com esse conhecimento que adquirimos.
Sobre o curso Data Analysis: estatística com Google Sheets
O curso Data Analysis: estatística com Google Sheets possui 117 minutos de vídeos, em um total de 41 atividades. Gostou? Conheça nossos outros cursos de Data Science em Data Science, ou leia nossos artigos de Data Science.
Matricule-se e comece a estudar com a gente hoje! Conheça outros tópicos abordados durante o curso:
- Probabilidade
- Análises e dilemas
- Medidas
- Médias pitagóricas
- Churn