Data Science: testando hipóteses
Conhecendo a metodologia - Apresentação
Deseja analisar amostras e aplicar testes de hipóteses para aprimorar seus conceitos de Data Science?
Meu nome é Ana Duarte e sou instrutora da Escola de Dados.
Audiodescrição: Ana é uma mulher de pele clara e olhos castanhos. Também tem cabelos castanhos ondulados na altura dos ombros. Usa um piercing no septo e está usando uma sombra laranja nos olhos. Está vestindo uma blusa azul marinho com a logo Alura estampada na cor branca. Na frente dela tem um microfone e atrás dela tem um vaso de planta, no lado esquerdo, e uma estante cheia de objetos decorativos, no lado direito. Ao fundo, uma parede iluminada por luzes de led nas cores verde e azul.
O que vamos aprender
Convido você a entender o que será abordado neste curso.
Nós vamos aplicar vários testes de hipóteses em diferentes cenários. Seremos consultores de Data Science para atuar em diversos projetos. Dessa forma, vamos entender:
- Testes de hipóteses para uma amostra;
- Testes de hipóteses para duas amostras;
- Testes não paramétricos.
Você já domina a análise exploratória e sabe analisar variáveis quantitativas e qualitativas? Então, este curso é para você aprofundar ainda mais seus conhecimentos em Data Science.
Aceita o desafio?
Então, esperamos você nos próximos passos!
Conhecendo a metodologia - Extraindo conclusões válidas
Então, nós somos consultores em uma empresa de data science. A ideia é trabalhar com vários clientes, em contextos diferentes, e auxiliar na tomada de decisão estratégica, utilizando as ferramentas que serão analisadas neste curso.
Atuando com a primeira empresa cliente
Nossa primeira empresa cliente é uma indústria de lâmpadas, e nossa missão é avaliar se fecharemos um novo contrato com ela. Nos convidaram para uma apresentação da equipe de análise exploratória, outra equipe da nossa empresa, que estava finalizando a entrega do contrato com várias análises dos dados que temos na empresa.
Temos dados como a idade da aposentadoria, para entender e coletar informações sobre se as pessoas estão se aposentando mais cedo na indústria. Temos também o tempo de vida das lâmpadas, para questões de garantia e entender quanto tempo, em média, uma lâmpada dura. E temos a altura das pessoas funcionárias, para proporcionar um ambiente mais ergonômico e entender melhor essas pessoas.
No meio da apresentação, que trazia vários histogramas sobre esses três aspectos da indústria, surgiu uma dúvida por parte da empresa cliente e das pessoas cientistas de dados. A cliente perguntou se poderíamos trazer informações válidas a partir dessas amostras que estão sendo analisadas. Essa pode ser a nossa deixa para impressionar a empresa cliente e, quem sabe, fechar um novo contrato.
Trabalhando com os dados levantados
Sugerimos à empresa cliente que façamos várias amostras dessas distribuições e comparemos a média dessas amostras com a média das distribuições originais para ver se são semelhantes. Vamos para o Google Colab para entendermos o que a equipe de análise exploratória fez e reproduzir essa sugestão.
No Colab, deixei um notebook pré-preenchido para você fazer o download na atividade "Preparando o ambiente". Nele tudo o que vamos ver no nosso curso, já bem esquematizado, como alguns códigos prontos, que não vamos focar.
O primeiro que aparece é o carregamento de bibliotecas que sempre usamos. Nele temos o numpy, o pandas e o matplotlib. Veremos outras bibliotecas ao longo desse curso, mas começamos já temos essas no início desse notebook.
# carregando bibliotecas
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
Temos também a leitura do CSV dos dados de idade de aposentadoria, do tempo de vida das lâmpadas e das alturas.
#Leitura dos dados
# idade de aponsentadoria
dados_idade_aposentadoria = pd.read_csv("/content/dados_idade_aposentadoria.csv")
# Tempo de Vida de uma Lâmpada
dados_vida_lampada = pd.read_csv("/content/dados_vida_lampada.csv")
# Altura dos funcionarios
dados_alturas = pd.read_csv("/content/dados_alturas.csv")
Vamos fazer o carregamento desses dados com você. No Colab, abrimos a coluna "Arquivos", à esquerda. Depois, no computador, abrimos a área de trabalho e arrastamos o arquivo dados_vida_lampadas.csv para a coluna "Arquivos" do Colab.
Repetiremos o processo para dados_idade_aposentadoria.csv e dados_alturas.csv. E agora que tudo já está carregado, posso executar a célula que já estava pré-preenchida com a leitura. Feito isso, podemos minimizar a coluna de arquivos.
Temos agora outra célula com # várias distribuições. Não se preocupem em como esses subplots foram criados, precisamos apenas focar na análise dos gráficos. Portanto, vamos apenas executar a célula pare gerar esses gráficos.
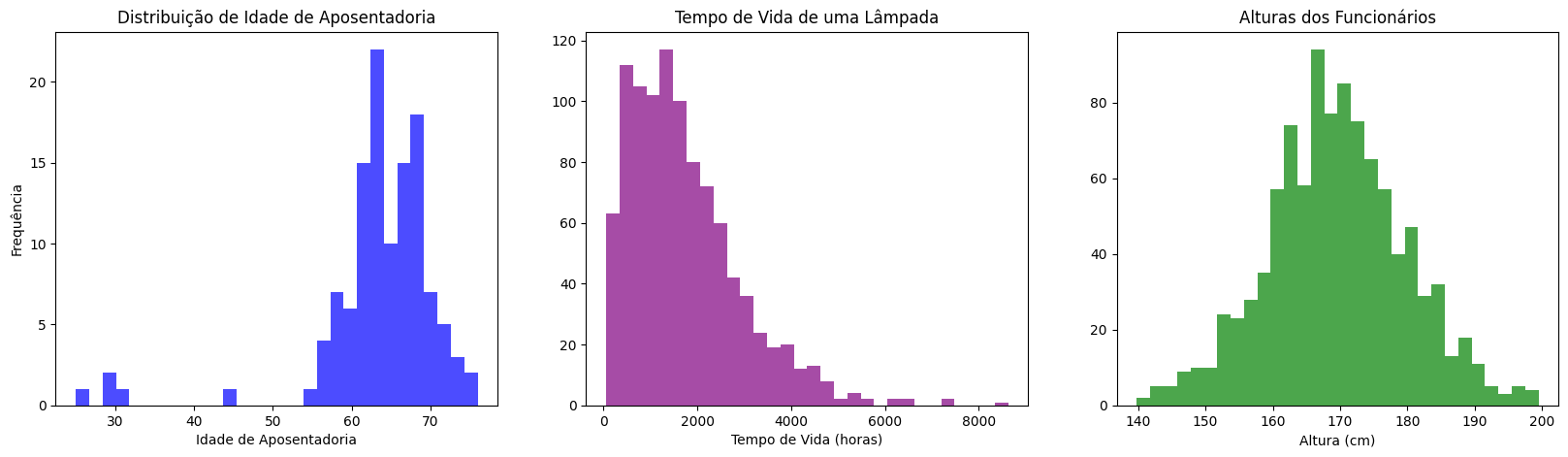
Se olharmos a distribuição da idade das aposentadorias, temos uma média de 62 anos, mais ou menos, mas temos algumas pessoas se aposentando mais cedo, apesar de não sabermos o motivo. Temos também o tempo de vida da lâmpada, com algumas lâmpadas que duram menos e algumas que duram mais, mas em menor frequência. E a altura dos funcionários, com uma média bem centralizada de, mais ou menos, uns 70 ou 69 anos.
São formatos diferentes de gráficos, então, o que precisamos fazer para responder o nosso cliente? Podemos trazer uma reamostragem. Queremos trazer várias amostras e comparar as médias de cada uma dessas distribuições.
Criando uma reamostragem
Vamos começar a fazer isso. Após os gráficos, teremos uma célula do notebook para a reamostragem, mas que está apenas com comentários.
# Reamostragens
# tamanho da amostra
# quantidade de amostras
# função de reamostragem e cálculo de médias
Primeiro coisa que definiremos é o tamanho da amostra, que será n=100. Isso significa que queremos 100 amostras de idade, 100 de tempos de vida de lâmpada e 100 de alturas. Em seguida, definimos quantas amostras queremos, e podemos colocar um número bem grande, como 100 mil (100000), por exemplo.
# Reamostragens
# tamanho da amostra
n = 100
# quantidade de amostras
qnt = 100000
# função de reamostragem e cálculo de médias
Agora que já definimos o tamanho da amostra e a quantidade de amostras, podemos criar uma função de reamostragem para otimizar os nossos procedimentos aqui no Colab. Usaremos essa função para fazer a reamostragem nas idades da aposentadoria, no tempo de vida e na altura.
Abaixo do comentário # função de reamostragem e cálculo de médias, vamos escrever uma função genérica:
# função de reamostragem e cálculo de médias
dados[coluna].sample(n, replace = true).mean()for _ in range(qnt)
Portanto, preciso dos dados, nos quais selecionaremos a coluna para reamostragem. Usaremos o método sample e, dentro dele, indicamos quantas amostras precisamos (n) e um replace, para podermos colocar observações repetidas. Depois que já fiz a amostragem, vou coletar a média dessas amostras, então chamamos o método mean().
Só que não queremos apenas uma amostra, mas várias amostras. Para isso, usaremos um looping com a ajuda do for. Usamos o underline (_), que é uma variável que não vamos acessar, e passamos o range(qnt) para o looping acontecer 100 mil vezes. Adicionamos tudo isso entre colchetes para armazenar essas informações em uma lista que está salva na variável medias.
# função de reamostragem e cálculo de médias
medias = [dados[coluna].sample(n, replace = true).mean()for _ in range(qnt)]
Como queremos definir como uma função, na linha acima de medias, precisamos usar o def e passar um nome para essa função. No caso, será reamostragem_medias(), que é o que estamos fazendo aqui. Essa função precisa receber os dados, a coluna, o tamanho da nossa amostra (n) e quantas vezes será rodada essa amostra (qnt). No final, escrevemos dois pontos (:) para definir como função. Por fim, precisamos retornar essas médias, então escrevemos return medias.
# Reamostragens
# tamanho da amostra
n = 100
# quantidade de amostras
qnt = 100000
# função de reamostragem e cálculo de médias
def reamostragem_media(dados, coluna, n, qnt):
medias = [dados[coluna].sample(n, replace=True).mean() for _ in range(qnt)]
return medias
Agora vamos executar essa célula para definir a nossa função. Em seguida, na célula abaixo, aplicaremos essa função em cada uma dessas distribuições. Começamos com a idade (media_idade). Para garantir que o nome dos dados está certo, copiamos o nome da célula # Leitura dos dados, no caso, dados_idade_aposentadoria.
E para descobrir o nome da coluna, em uma nova célula, rodamos o código daods.head(). Por exemplo, dados_idade_aposentadoria.head(), e descobrimos que o nome da coluna é idade.
dados_idade_aposentadoria.head()
| # | idade |
|---|---|
| 0 | 66 |
| 1 | 66 |
| 2 | 60 |
| … | … |
O tamanho da amostra e quantidade de amostragem já temos registado. Então ficou:
# Realizando as reamostragens com a função
medias_idade = reamostragem_media(dados_idade_aposentadoria, 'idade', n, 1000)
Depois, basta copiar a linha de código e repetir o processo para descobrimos a média de duração das lâmpadas e a média de altura das pessoas funcionárias.
# Realizando as reamostragens com a função
medias_idade = reamostragem_media(dados_idade_aposentadoria, 'idade', n, 1000)
medias_duracao = reamostragem_media(dados_vida_lampada, 'duracao', n, qnt)
medias_altura = reamostragem_media(dados_alturas, 'alturas', n, qnt)
Já temos definida a aplicação da reamostragem em cada uma dessas distribuições. Ao executarmos a célula, demora um pouco para carregar o resultado, porque ele está colocando o looping em cada um dos CSVs.
Nos próximos passos, comparamos as médias originais com as médias que fizemos a reamostragem.
Conhecendo a metodologia - Conhecendo o TLC
Executamos a re-amostragem de diversas idades, alturas e durações de lâmpadas da nossa indústria. Precisamos responder à pergunta da empresa cliente: é possível obter informações válidas de uma amostra?.
Analisando a validade dos dados de uma amostra
Para isso, comparamos as médias populacionais com as médias retiradas desse experimento. Em uma nova célula do Colab, vamos coletar as médias originais, porque já temos as médias populacionais. Então vamos escrever print("idade"), para fazermos a média de idade.
Precisamos trazer a média original, que está em dados_idade_aposentadoria. Então vamos selecionar a coluna ['idade'] e aplicar a função mean(). Feito isso, podemos imprimir os dados.
print("***** Médias populacionais *****")
print("idade:", dados_idade_aposentadoria['idade'].mean())
***** Médias populacionais *****
idade: 62.70857142857143
Na nossa indústria, as pessoas estão se aposentando, em média, aos 62 anos. Agora vamos entender qual é a duração média das lâmpadas. Podemos copiar o print(), colar na linha abaixo e fazer as mudanças:
- de
dados_idade_aposentadoriaparadados_vida_lampada; - de
['idade']para['duracao'].
Dica: Copiar e colar o nome dos bancos de dados e variáveis ajuda a evitar um erro trabalhoso do Colab. Sempre que possível, use essa prática.
print("***** Médias populacionais *****")
print("idade:", dados_idade_aposentadoria['idade'].mean())
print("duração:", dados_vida_lampada['duracao'].mean())
***** Médias populacionais *****
idade: 62.70857142857143
duração: 1731.8036029420002
Ao imprimirmos, descobrimos que as lâmpadas duram, em média, 1.732 horas. Por fim, vamos descobrir qual é a altura média dos funcionários, a partir dos dados_altura. Assim, descobrimos que, em média, as pessoas têm 1,69 metros de altura.
print("***** Médias populacionais *****")
print("idade:", dados_idade_aposentadoria['idade'].mean())
print("duração:", dados_vida_lampada['duracao'].mean())
print("altura:", dados_alturas['alturas'].mean())
***** Médias populacionais *****
idade: 62.70857142857143
duração: 1731.8036029420002
altura: 169.52022
Comparando médias populacionais e amostrais
Agora podemos comparar as médias amostrais para ver se estão próximas. Para isso, copiaremos as linhas de print() que acabamos de criar e colaremos na célula de baixo, onde temos o Avarage(), assim otimizamos nosso código. Contudo, ao invés das distribuições originais, vamos fazer as distribuições das médias, ou seja, substituiremos a fonte dos dados pelas médias.
Além disso, já temos o método Average(), então não vamos usar o mean(), porque não estamos tratando de um dataframe, e sim de uma lista. Por isso usamos o Average(), que está, basicamente, somando todos os valores e dividindo pelo tamanho, que é a fórmula da média.
def Average(lst):
return sum(lst) / len(lst)
print("***** Médias pamostrais *****")
print("idade:", Average(medias_idade))
print("duração:", Average(medias_duracao))
print("altura:", Average(medias_altura))
***** Médias pamostrais *****
idade: 62.71138789999943
duração: 1731.7091029524452
altura: 169.51718177700027
Agora, precisamos fazer a comparação das médias da distribuição original com as que obtivemos. Se observarmos, temos uma diferença nas casas decimais.
Tabela de comparação:
| Dado | Média populacional | Média amostral |
|---|---|---|
| idade | 62.70857142857143 | 62.703779600000266 |
| duração | 1731.8036029420002 | 1732.8779010336582 |
| altura | 169.52022 | 169.49994350000064 |
Na duração original, as lâmpadas duram, em média, 1.731 horas, e, na amostragem, a média foi de 1.732 horas. Portanto, temos diferenças muito pequenas entre as médias amostrais e as médias originais. Voltamos à pergunta da nossa empresa cliente, podemos, sim, tirar conclusões válidas a partir das nossas amostras, até porque as médias amostrais estão bem parecidas com as médias originais.
Entendendo a distribuição da média
Para finalizar, podemos dar uma olhada na distribuição dessas médias. Para isso, tenho o código pronto com os subplots, porque a ideia não é saber como construí-lo, mas sim analisar os gráficos. Vamos apenas inserir a fonte de dados, ou seja, a media_idade, a media_duracao e a media_altura.
plt.subplots(figsize=(15, 5))
plt.subplot(131)
plt.title('Distribuição das Idade médias de Aposentadoria')
plt.xlabel('Idade média de Aposentadoria')
plt.ylabel('Frequência')
plt.hist(medias_idade, bins=30, alpha=0.7, color='blue')
plt.subplot(132)
plt.hist(medias_duracao, bins=30, alpha=0.7, color='purple')
plt.title('Duração média de uma Lâmpada')
plt.xlabel('Tempo de Vida médio(horas)')
plt.subplot(133)
plt.hist(medias_altura, bins=30, alpha=0.7, color='green')
plt.title('Alturas média dos Funcionários')
plt.xlabel('Altura média (cm)')
plt.show()
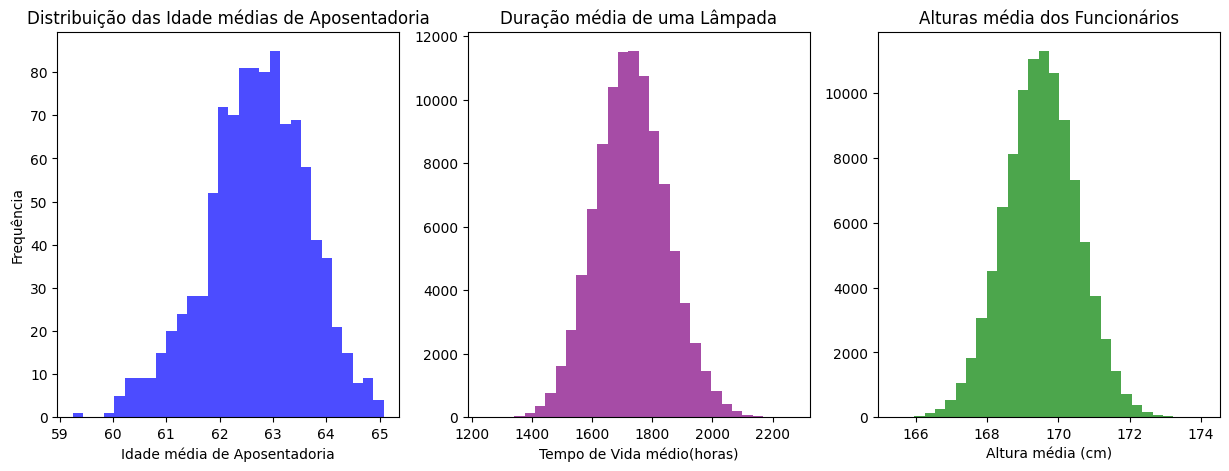
Quando olhamos os gráficos, reparem que temos distribuições bem parecidas para cada uma delas, o que é curioso, porque, originalmente, no nosso gráfico populacional, elas têm formatos bem diferentes.

Esse formato de distribuições que é um sino, que é uma solução, tem uma raiz em um teorema muito utilizada dentro da estatística: Teorema do Limite Central. Esse teorema é famoso na estatística para fazermos inferências, ou seja, generalizar a partir de uma amostra para uma população. Vamos deixar uma atividade para você explorar melhor esse tema.
Portanto, podemos informar para empresa cliente que podemos, sim, fazer essas conclusões com base nessa amostra, baseado nesse Teorema do Limite Central. Agora podemos atuar com outros projetos, pois fechamos um contrato com nossa cliente da indústria de lâmpadas.
Sobre o curso Data Science: testando hipóteses
O curso Data Science: testando hipóteses possui 110 minutos de vídeos, em um total de 53 atividades. Gostou? Conheça nossos outros cursos de Data Science em Data Science, ou leia nossos artigos de Data Science.
Matricule-se e comece a estudar com a gente hoje! Conheça outros tópicos abordados durante o curso:
- Conhecendo a metodologia
- Teste para uma amostra grande
- Teste para uma amostra pequena
- Testes para suas amostras
- Testes não paramétricos