Estatística com Python: probabilidade e amostragem
Distribuição binomial - Introdução
Boas vindas a mais um treinamento da Plataforma Alura!
Sou o instrutor Rodrigo Dias neste curso de Estatística com Python parte 2: Probabilidade e Amostragem, o qual faz parte de uma sequência lógica sobre este tema.
No primeiro curso, começamos a falar de estatísticas descritivas e de coisas mais básicas, mas agora evoluiremos um pouco mais; conheceremos algumas Distribuições de Probabilidade e aprenderemos a calculá-las, como a distribuição binomial, a distribuição Poisson e a famosa distribuição normal.
Também falaremos um pouco sobre o conceito de Amostragem, e calcularemos e obteremos uma amostra aleatória simples utilizando recursos do Pandas.
Abordaremos técnicas de Amostragem, e depois passaremos para Estimação ainda no universo de inferência estatística, onde veremos estimações pontuais e intervalares.
Aprenderemos a calcular o tamanho de amostra para obtermos amostras representativas da população que estamos estudando.
Falaremos de erro inferencial, nível de confiança, nível de significância, teorema do limite central e todos esses conceitos importantes em Estatística pra termos uma bagagem sólida para avançarmos mais ainda, chegando em teste, regressão linear e etc.
Esse treinamento é focado nessa parte mais intermediária. Esperamos que gostem.
Vamos lá!
Distribuição binomial - Conhecendo o ambiente e o dataset
Inicialmente, apresentaremos a ferramenta Colaboratory do Google conhecida como Colab, a qual é acessível por meio deste link, sendo a mesma que utilizamos no curso anterior.
Precisaremos fazer login para fazermos upload dos arquivos disponibilizados no passo anterior, do mesmo jeito que já fizemos.
Feito o download dos documentos, abriremos o Colab no navegador, iremos em "File > Upload notebook...", e escolheremos o arquivo Versão_bibliotecas.ipynb. Abrindo-o para rodarmos a célula já pronta, verificaremos as versões das bibliotecas Pandas, Numpy, Scipy e Matplotlib que utilizaremos.
Versão do pandas -> 0.23.4
Versão do numpy -> 1.16.2
Versão do scipy -> 1.2.1
Versão do matplotlib -> 3.0.3Provavelmente sua versão será mais recente, mas se tiver algum problema enquanto estiver executando o código, poderá voltar e fazer o downgrade no Colab conforme aprendemos na primeira aula do primeiro curso de Estatística, caso haja dúvidas.
Expandiremos a aba lateral para começarmos carregando o arquivo dos dados que utilizaremos em nosso projeto; clicaremos em "upload" e escolheremos dados.csv, o qual é o mesmo dataset criado no curso anterior.
Não o utilizaremos muito neste treinamento, mas ao final teremos um notebook para executarmos um projeto de exercício usando o que aprendemos durante as aulas.
Feito o carregamento dos dados, abriremos o notebook preparado para este curso indo em "File > Upload Notebook..." novamente para escolhermos o arquivo Curso_de_Estatística_Parte_2.ipynb.
Este possui um roteiro para executarmos nossas aulas; na primeira parte, já conhecemos o mesmo dataset do curso anterior, o qual foi extraído do site oficial do IBGE e possui os dados da Pesquisa Nacional por Amostra de Domicílios de 2015 ou PNAD.
Encontraremos o link com a fonte dos dados, bem como as variáveis que vamos utilizar; renda, idade das pessoas, a altura elaborada didaticamente para estudarmos uma distribuição que se comporta de forma normal, como veremos neste treinamento. Temos também as codificações numéricas das Unidades da Federação, sexo, anos de estudo e cor ou raça.
Teremos algumas observações de tratamentos realizadas no dataset único e exclusivamente para facilitar nosso aprendizado; pois eliminamos tanto os registros de renda inválidos quanto os inexistentes ou missing, e consideramos somente as pessoas de referência que foram entrevistadas e são responsáveis pelo domicílio.
Os registros das observações são importantes para entendermos bem os resultados finais. Em seguida, importaremos o dados.csv que já deve estar carregado na aba lateral de "Files".
Na primeira célula da parte "Importando pandas e lendo o dataset do projeto", começaremos com o import de pandas como pd, da mesma forma que já conhecemos.
import pandas as pdArmazenaremos os dados na variável dados, a qual será igual a pd.read_csv() recebendo o arquivo 'dados.csv' para o lermos.
dados = pd.read_csv('dados.csv')Após rodarmos esta célula com "Shift + Enter", exibiremos os primeiros cinco registros com head().
dados.head()| UF | Sexo | Idade | Cor | Anos de Estudo | Renda | Altura | |
|---|---|---|---|---|---|---|---|
| 0 | 11 | 0 | 23 | 8 | 12 | 800 | 1.603808 |
| 1 | 11 | 1 | 23 | 2 | 12 | 1150 | 1.739790 |
| 2 | 11 | 1 | 35 | 8 | 15 | 880 | 1.760444 |
| 3 | 11 | 0 | 46 | 2 | 6 | 3500 | 1.783158 |
| 4 | 11 | 1 | 47 | 8 | 9 | 150 | 1.690631 |
Já conhecemos a ferramenta e o dataset que vamos utilizar um pouco nesse curso.
A seguir, vamos colocar a mão na massa e falar das Distribuições Teóricas de Probabilidade.
Distribuição binomial - Distribuição binomial
Iniciaremos de fato nosso curso abordando as Distribuições Teóricas de Probabilidade.
Quando avaliamos a forma como a variável aleatória se distribui, conseguimos definir diferentes tipos de Distribuições de Frequência ou de Probabilidade, como vimos no curso anterior a este.
Neste primeiro passo, falaremos sobre as três importantes que são muito utilizadas em estatística: Binomial, a Poisson e a famosa Normal.
Começaremos lidando com alguns problemas, e depois tentaremos encaixá-los nas Distribuições para solucioná-los.
Em um concurso para preencher uma vaga de Cientista de Dados, temos um total de 80 questões de múltipla escolha, cada uma com três alternativas possíveis. Estas têm o mesmo valor, e suporemos que um candidato que não tenha estudado absolutamente nada resolva fazer a prova e chute todos os resultados.
Assumindo que a prova vale 10 pontos e que a nota de corte é 5, ou seja, passará se sua nota for 5 ou mais e reprovará se for menos que 5, qual seria a chance deste candidato passar para próxima etapa do processo seletivo?
Resolveremos problemas desse tipo utilizando a Distribuição de Probabilidade Binomial.
Em nosso notebook, há um pequeno texto com explicação dessa Distribuição contendo a fórmula e o que representa cada item da fórmula para usarmos como material de consulta.
Um Evento Binomial é caracterizado pela possibilidade de ocorrência de apenas duas categorias; ou é sim ou é não, verdadeiro e falso, sucesso ou fracasso e etc.
A soma dessas duas categorias é o Espaço Amostral, ou seja, o total de eventos possíveis dentro de um experimento.
Por exemplo, o lançamento de uma moeda pode ter a face "cara" ou a "coroa", e esse é o Espaço Amostral com duas possibilidades.
Em outro exemplo de um lançamento de dado de seis faces, só poderemos ter seis resultados possíveis: 1, 2, 3, 4, 5, ou 6.
Na fórmula, teremos a probabilidade de ocorrer k representada por P vezes k, o qual é um número de eventos desejados que tenham sucesso.
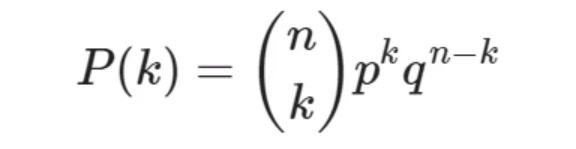
O n sobre k entre parênteses é a combinação de n combinados de k em k, o que é um método matemático bem simples de resolver, e temos um método no Python que fará este cálculo. Mais adiante, teremos p da probabilidade de sucesso elevado a k.
Por exemplo, se estivermos estudando o número de "caras" que ocorrem no lançamento de uma moeda, queremos saber a probabilidade de ocorrer esta face, que obviamente seria de 50% por haver somente duas situações possíveis.
Já o elemento q é igual a 1 menos p representando a probabilidade de fracasso. No caso da moeda, seria a probabilidade de obter "coroa" de 50% também.
A soma das probabilidades p mais q será igual a 1 ou 100%, e o resultado variará de 0 a 1 dependendo do caso.
Por fim, n é o número de eventos estudados. Em nosso exemplo das 80 questões em uma prova cuja nota máxima é 10 e a nota de corte é 5, o candidato deverá acertar pelo menos 40 questões, ou seja, a metade que corresponde à nota de corte.
Com isso, o n seria 80 e o k seria 40 para o número de eventos mínimos necessários para o candidato ter sucesso.
O Experimento Binomial tem etapas que o caracterizam, e se as seguirmos, conseguiremos identificar se o problema pode ser resolvido utilizando Distribuição Binomial ou não.
Primeiro, faremos a realização de n ensaios idênticos, como quando jogamos uma moeda; a chance de cair "cara" é de 50% e a "coroa" de 50% também, e isso acontecerá da mesma maneira nos demais lançamentos.
Os ensaios também são independentes entre si, e temos somente dois resultados possíveis como já falamos.
A probabilidade de sucesso é representado por p e a de fracasso por q igual a 1 menos p, e não se modificam de ensaio para ensaio em nosso caso, mas claro que há situações em que isso não ocorrerá.
Já a média da Distribuição Binomial é representado por μ igual a n vezes p e o Desvio Padrão por σ igual a raiz quadrada de n vezes p vezes q.
De volta ao notebook, teremos a parte "Importando bibliotecas" onde deveremos importar o comb da biblioteca sipy.special para podermos calcular a combinação de n de k a k representada por Cnk ou n sobre k entre parênteses.
from scipy.special import combNesta parte, também encontraremos um link com a documentação do Scipy, contendo informações sobre a funcionalidade comb() que utilizaremos, a qual é justamente o método que resolverá a combinação.
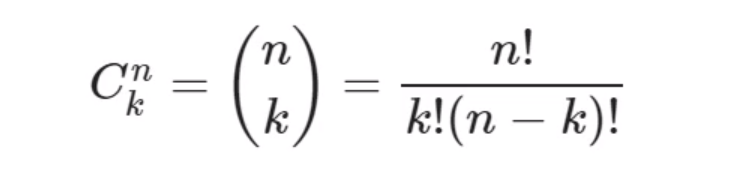
Por exemplo, temos 4 amigos e queremos combiná-los em pares; para isso, poderemos pegar o primeiro com o segundo, depois o primeiro com o terceiro, o primeiro com o quarto, o segundo com o terceiro, o segundo com o quarto, e por fim o terceiro com o quarto. Logo, teremos 6 possibilidades diferentes.
A fórmula da combinação nos dará esta resposta com a operação de n fatorial ou n! - que é o produto de uma contagem regressiva - sobre k fatorial ou k! vezes a subtração fatorial de n menos k ou (n-k)!.
Se temos 5 fatorial ou 5!, o resultado da operação é 5 vezes 4 vezes 3 vezes 2 vezes 1, ou seja, é o produto da multiplicação de uma contagem regressiva. Vale lembrar que, por definição, 0 fatorial ou 0! é igual a 1.
Em um exemplo prático bem simples da loteria Mega Sena que tem 60 números, descobriremos a probabilidade de ganhar este prêmio. Já que temos um total de 1 a 60 números para escolher onde a aposta mínima é 6 números, deveremos descobrir o Espaço Amostral e as possibilidades por meio da Combinação.
Temos apenas uma chance de ganhar na Mega Sena, e precisamos calcular "1" dividido pelo Espaço Amostral, o qual é justamente a combinação de 60 números de 6 em 6.
Usando o Python, aplicaremos a operação na parte "Exemplo: Mega Sena" de nosso notebook. Na primeira célula, criaremos a variável combinacoes sendo igual a comb() recebendo os valores 60 e 6. Para recebermos os resultados, chamaremos apenas combinacoes em seguida.
combinacoes = comb(60, 6)
combinacoesComo retorno, teremos o valor de 50063860.0 resultados ou combinações possíveis.
Para calcularmos a probabilidade de ganharmos o prêmio com apenas um bilhete, criaremos a variável probabilidade sendo igual a 1 dividido pela operação anterior.
Em seguida, exibiremos o resultado chamando probabilidade.
probabilidade = 1 / combinacoes
probabilidadeComo será um valor muito pequeno, formataremos o retorno com print() recebendo '%0.15f' entre aspas simples para quinze casas decimais seguido de % e probabilidade para plotarmos em percentual.
probabilidade = 1 / combinacoes
print('%0.15f' % probabilidade)Portanto, a chance de ganharmos na Mega Sena é bem pequena, cerca de 0,0000000199%. Aplicando à fórmula, teremos a combinação de 60 de seis em seis números, sendo igual a 60 fatorial OU 60! dividido por 6 fatorial que é multiplicado pela subtração fatorial de 60 menos 6.
A seguir, pegaremos o problema que começamos e o resolveremos utilizando a distribuição binomial.
Sobre o curso Estatística com Python: probabilidade e amostragem
O curso Estatística com Python: probabilidade e amostragem possui 183 minutos de vídeos, em um total de 74 atividades. Gostou? Conheça nossos outros cursos de Estatística em Data Science, ou leia nossos artigos de Data Science.
Matricule-se e comece a estudar com a gente hoje! Conheça outros tópicos abordados durante o curso:
- Distribuição binomial
- Distribuição de Poisson
- Distribuição normal
- Técnicas de amostragem
- Nível e intervalo de confiança
- Calculando o tamanho da amostra
- Resumo e projeto final