Estatística com R: aplicando a probabilidade e a amostragem dos dados

Distribuição Binomial - Apresentação

Já pensou em como a estatística pode ser aplicada na análise de dados e sua importância na carreira de um cientista de dados? Se quer aprender a usar conceitos estatísticos para resolver problemas e desenvolver um projeto em R para enriquecer seu portfólio, este é o lugar certo para você!

Vamos aprender sobre isso nesse curso de Estatística com R, utilizando a probabilidade e a amostragem.

Audiodescrição: Alfonso Rios é um homem de pele morena, tem cabelos e olhos castanhos. Usa barba, uma camiseta escura e fones de ouvido sem fio. Ao fundo, uma iluminação verde, além de uma parede lisa com uma prateleira na parte superior e uma porta à esquerda.

Neste curso, atuaremos como cientistas de dados em uma consultoria que presta serviços para empresas de diversas áreas. Nosso foco será utilizar conceitos de estatística para investigar e auxiliar nos problemas e demandas de algumas empresas, baseando suas decisões nas análises de dados.

Para isso, precisaremos compreender as diferenças entre as distribuições de probabilidades e suas aplicações. Exploraremos problemas e investigaremos qual tipo de distribuição é adequada para resolver cada tipo de problema. Calcularemos probabilidades e estimaremos resultados baseados na estatística para casos relacionados a cada tipo de problema que uma empresa pode enfrentar.

Aprenderemos a gerar insights e levantar hipóteses de acordo com os dados que estamos analisando. Por fim, realizaremos a amostragem visando obter resultados dos dados em relação à população, reduzindo custos financeiros e de recursos. Tentaremos trabalhar de forma a não precisar usar todos os dados para conseguir resultados semelhantes, utilizando menos dados.

Para isso, teremos acesso a resultados de pesquisa e dados fornecidos por algumas dessas empresas, seja do time de marketing, atendimento ao cliente, vendas, logística, entre outros.

Pré-requisitos

Para acompanhar este curso da melhor forma, é importante ter pelo menos um conhecimento básico em R, especialmente na biblioteca R Basic. Também é importante conhecer conceitos primordiais de estatística, como tipos de variáveis, distribuição de frequência, medidas de tendência central (média, mediana e moda), medidas separatrizes (quartis, quantis e percentis) e medidas de dispersão, como o desvio padrão.

Todo esse conhecimento é essencial para construirmos nosso projeto.

Com as expectativas alinhadas, vamos começar nosso projeto?

Distribuição Binomial - Iniciando o projeto

Vamos atuar como cientistas de dados em uma consultoria que presta serviços a empresas de diversas áreas. Como desafio, precisamos utilizar conceitos de estatística e análise de dados para resolver casos que possam auxiliar nos processos de decisão e geração de insights dos nossos clientes. Para isso, teremos acesso aos resultados de pesquisas e dados de diferentes equipes dessas empresas, como marketing, atendimento, logística, entre outros.

Nosso foco é utilizar os conceitos de estatística atrelados à linguagem R para resolver esses casos e também entender de onde partimos e para onde vamos com essas análises.

Ferramentas e ambiente de trabalho

Para realizar as análises de cada caso, utilizaremos um documento no Jupyter Notebook, um Colab do Google que trará todo passo a passo para resolver esses casos. Tudo está bem documentado para que possamos estudar ao observar todos os dados.

Primeiramente, é importante verificar se o documento está pronto para uso. Para isso, ao acessar o Colab, na barra de menu superior, clicamos na aba "Editar > Configurações de notebook". Na janela que abre, encontramos o campo Tipo de ambiente em execução. Precisamos verificar se a opção selecionada é a "R". Se sim, clicamos no botão "Salvar". Caso não, selecionamos essa opção e salvamos.

No documento, há um resumo explicando nosso cenário e projetos. Na primeira célula, temos a importação de pacotes para o projeto, incluindo dplyr, para manipulação de dados, e o ggplot2, para visualização dos dados. Também limitamos a exibição dos dados a no máximo 10 linhas, caso necessário. Sabendo disso, executamos a célula.

# Importando os pacotes do projeto
library(dplyr)
library(ggplot2)
options(repr.matrix.max.rows = 10)

Esses são apenas alguns dos pacotes que utilizaremos, pois as principais ferramentas estatísticas fazem parte do pacote R Basic e da biblioteca Stats, já pré-carregados no Colab Notebook.

Muitas das ferramentas estatísticas que utilizaremos se baseiam em probabilidade. A probabilidade mede o quão provável é um evento ocorrer, variando de 0 (nunca ocorre) a 1 (sempre ocorre). Por exemplo, se a probabilidade de chover em uma cidade é de 30%, significa que em 100 casos, em 30 deles, é provável que chova. A probabilidade é menor do que o esperado, mas existe, podendo chover em algum caso naquele dia.

A probabilidade é útil ao trabalharmos com dados, pois variáveis como idade, sexo biológico, altura e renda são aleatórias, variando ao acaso. Uma distribuição de probabilidade descreve como essas variáveis podem estar distribuídas. Neste curso, aprenderemos sobre três distribuições: binomial, de Poisson e normal, conforme mostrado no notebook.

Em estatística, cada distribuição de probabilidade tem sua própria forma e pode ser utilizada para modelar diferentes tipos de eventos aleatórios. O tipo de distribuição pode explicar como cada variável se distribui. Para aprendermos sobre cada uma delas, responderemos a questionamentos e casos onde identificaremos qual experimento está presente em cada distribuição e como resolver e calcular essas probabilidades e valores esperados de acordo com o comportamento.

Próximos passos

Agora que importamos os pacotes do R e entendemos sobre probabilidade, vamos começar a resolver os casos, procurando saber o que precisamos encontrar, quais são os dados disponíveis e o que desejamos descobrir com esses dados.

Distribuição Binomial - Calculando as combinações possíveis

Estamos agora com nosso primeiro case que envolve a Zoop, uma empresa de comércio varejista. No início do arquivo, temos um enunciado que traz a combinação de ofertas de produtos.

A empresa, Zoop, está planejando uma grande campanha promocional para impulsionar as vendas de fim de ano, incluindo pacotes de produtos para promoções tanto da Black Friday quanto do Natal. Para isso, o time de marketing decidiu combinar diferentes produtos em pacotes atrativos. A campanha envolve dez produtos diferentes, criando pacotes promocionais de três produtos cada. O time de marketing precisa saber quantas dessas combinações de pacotes são possíveis e como calcular esse valor.

Combinação sem repetição

O segredo está na palavra "combinação". Como estamos combinando produtos, podemos utilizar o conceito de combinação sem repetição. Suponhamos que, desses dez produtos, tenhamos um liquidificador, uma airfryer e uma cafeteira. Se invertermos a ordem para liquidificador, cafeteira e airfryer, continuará sendo o mesmo pacote. Portanto, não precisamos de repetição, por isso utilizamos o conceito de combinação sem repetição.

Fórmula da combinação e cálculo com R

Para calcular isso, como seriam várias combinações e seria necessário ter cuidado, existem fórmulas matemáticas que fazem esse processo.

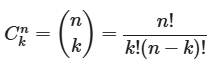
A fórmula da combinação diz o seguinte: para encontrar combinações de N objetos tomados K a cada vez, ou seja, dez produtos tomados três produtos cada, como no nosso exemplo, utilizamos a combinação 10, 3 a 3. Isso envolve o cálculo do fatorial, que é o símbolo de exclamação seguido do número.

Não se preocupe, pois haverá uma atividade explicando sobre combinação e fatorial. Nosso foco é entender como calcular isso utilizando as funções do R e os conceitos de estatística por trás desses problemas.

Para resolver esse problema, utilizaremos a função choose do R. Você pode acessar o link que disponibilizamos na documentação para verificar como é seu funcionamento.

Como temos dez produtos e queremos três por pacote, se quisermos transformar isso na fórmula de combinação, seria no formato combinação 10, 3 a 3. Essa formatação pode ser colocada em uma calculadora ou utilizada em outros tipos de cálculos para chegar ao valor. No entanto, utilizaremos a função choose do R para resolver essa combinação.

No R, passaremos para o nosso N a quantidade de produtos que temos, que são 10 no nosso problema, e para o K o valor de 3, que é o número de produtos que queremos por pacote.

n <- 10 # nº de produtos
k <- 3 # nº de produtos por pacote

Vamos salvar esses dois valores. Para calcular a combinação, basta utilizar a função choose(), atribuindo o resultado a uma variável com o operador <-. A função choose recebe n que é a quantidade de objetos e k, a tomada do produto.

combinacoes <- choose(n,k)
combinacoes

120

Ao rodar esse código, vemos quantas combinações temos, nesse caso 120 combinações únicas de pacotes de três produtos, utilizando 10 produtos.

Calculando a probabilidade de escolha aleatória

Essa combinação é importante para o prosseguimento do nosso case. Por curiosidade, se quisermos saber a probabilidade de escolher aleatoriamente o pacote de produtos específico, como o de liquidificador, airfryer e cafeteira, calculamos a probabilidade considerando o caso desejado sobre o total de resultados possíveis.

No nosso cálculo, é 1, pois só temos essa combinação desejada, e o espaço amostral é 120. O espaço amostral representa todos os eventos possíveis, ou seja, todas as combinações dos produtos. Calculamos 1 sobre 120.

probabilidade <- 1/20
probabilidade

0.00833333333333333

Temos aproximadamente 0,83% de chance de escolher esse pacote aleatoriamente. É uma probabilidade baixa, mas normal, considerando as muitas possibilidades.

Com isso, descobrimos que a equipe de marketing da Zoop terá 120 combinações únicas de pacotes promocionais, escolhendo 3 produtos de um total de 10. Essa informação pode ser importante para que o time de marketing estabeleça estratégias para observar o desempenho de cada pacote, analisando se estão vendendo bem ou não.

Próximos passos

No próximo vídeo, aprenderemos como calcular a distribuição binomial, o que é um experimento binomial, como utilizá-lo e como calcular as probabilidades necessárias para os nossos cases, utilizando as combinações que já fizemos.

Sobre o curso Estatística com R: aplicando a probabilidade e a amostragem dos dados

O curso Estatística com R: aplicando a probabilidade e a amostragem dos dados possui 154 minutos de vídeos, em um total de 63 atividades. Gostou? Conheça nossos outros cursos de Estatística em Data Science, ou leia nossos artigos de Data Science.

Matricule-se e comece a estudar com a gente hoje! Conheça outros tópicos abordados durante o curso:

• Distribuição binomial
• Distribuição de Poisson
• Distribuição Normal
• Estimação
• Cálculo do tamanho da amostra