Estatísticas com R: testando modelos de regressão
Regressão linear múltipla - Apresentação
Você já se deparou com a necessidade de prever o valor de algo que depende de vários fatores ao mesmo tempo?
Vamos dar um exemplo, imagine que você queira estimar o valor de um automóvel. Para isso, você poderia usar características como o estilo do automóvel, se é um carro sedã, SUV, ano de fabricação, potência do motor, entre outras informações relevantes.
Neste curso, aprenderemos exatamente isso: como criar modelos de regressão com mais de uma variável preditora, ou seja, com múltiplas variáveis.
Antes de começarmos a falar sobre o projeto que desenvolveremos, vamos nos apresentar. Meu nome é Valquíria, sou instrutora na Escola de Dados.
Audiodescrição: Valquíria é uma mulher branca, de olhos castanhos, cabelos também castanhos e lisos, na altura abaixo dos ombros. Usa uma camiseta azul, piercing no septo e tem tatuagens nos dois braços. Ao fundo, uma parede lisa com iluminação degradê do azul para o verde. Ao lado direito, uma prateleira com objetos, como quadros e uma letra "A".
O que aprenderemos
Nesse curso desenvolveremos um projeto para uma empresa que vende automóveis usados. Atualmente, a precificação dos automóveis é feita manualmente, mas desejam automatizar esse processo e torná-lo mais confiável.
Portanto, criaremos um modelo de regressão que tenha o menor erro possível, para que essa empresa consiga utilizá-lo na precificação dos automóveis.
Para isso, começaremos com o modelo de regressão linear múltipla. No entanto, entenderemos que algumas variáveis não têm uma relação linear com o preço dos automóveis. Assim, começaremos a trabalhar com outros tipos de modelos.
Conheceremos as árvores de decisão, entenderemos como esse tipo de algoritmo funciona, suas vantagens e desvantagens, e aprofundaremos esse conhecimento para trabalhar com modelos de ensemble, que combinam várias árvores para chegar a um resultado mais robusto.
Falaremos sobre a técnica de bagging, aplicaremos o algoritmo de Random Forest e, por fim, trabalharemos com a técnica de Boosting, que cria vários modelos de árvores, sempre corrigindo o erro do anterior para chegar a um resultado ainda melhor.
No final, compararemos os resultados obtidos, utilizando diferentes métricas para escolher o modelo com melhor desempenho. Salvaremos esse modelo e aprenderemos como carregá-lo e utilizá-lo com novos dados.
Será uma experiência enriquecedora, e estamos animados para começar.
Pré-requisitos
Para acompanhar bem este curso, recomendamos que já tenhamos conhecimento de programação na linguagem R e também conhecimentos em regressão linear.
Vamos começar?
Regressão linear múltipla - Conhecendo e preparando os dados
Vamos dar início ao nosso projeto. Atuaremos como cientistas de dados para uma empresa que vende automóveis usados. O problema que enfrentam é a precificação manual dos automóveis, o que pode levar a inconsistências e falta de automação.
Nosso objetivo é criar um modelo de regressão que receba características dos automóveis e retorne o valor de venda com o menor erro possível. Exploraremos diferentes modelos de regressão até encontrar o que traga o menor erro, salvando-o para uso com novos dados da empresa.
Antes de começarmos, precisamos dos dados. A empresa forneceu alguns dados que carregaremos e exploraremos para entender o que temos antes de construir nosso modelo de regressão.
Estamos no ambiente do Google Colab, que por padrão é configurado em Python, mas trabalharemos em R. Para mudar a linguagem, vamos ao menu superior e clicamos em "Ambiente de execução > Alterar o tipo de ambiente de execução". Feito isso, mudamos o tipo de ambiente para "R". Clicamos no botão "Salvar".
Depois, na lateral superior direita da tela, clicamos no botão "Reconectar". Feito isso, podemos iniciar. A primeira coisa que faremos será carregar o pacote Tidyverse para conseguirmos analisar os dados e fazer a exploração.
Para isso, escrevemos library(tidyverse) e executamos a célula.
library(tidyverse)
Os dados estão no GitHub, em um repositório chamado testando_modelos_regressao, no arquivo automoveis_usados.csv. Para acessar os dados brutos, clicamos na parte superior direita da página do GitHub, no botão escrito "Raw". Feito isso, abre em uma janela as colunas e linhas do arquivo separados por vírgula. No campo de endereço, pressionamos "Ctrl + C" para copiar.
Voltamos ao Google Colab. Vamos armazenar esse endereço em uma variável, então, escrevemos url<- ''. Nas aspas, colamos o endereço e executamos a célula.
URL <- 'endereço_do_arquivo'
Após, vamos carregar os dados do endereço em uma nova variável dados usando a função read.csv.
dados <- read.csv(url)
Podemos visualizar as primeiras linhas usando a função head(dados).
head(dados)
| Estilo | Ano | Potencia_motor | Cilindros_motor | Consumo_estrada_km | Valor |
|---|---|---|---|---|---|
| SUV 4 portas | 2005 | 275 | 6 | 28.96812 | 29695 |
| seda | 2016 | 170 | 4 | 61.15492 | 30495 |
| minivan de passageiros | 2016 | 248 | 6 | 45.06152 | 37650 |
| seda | 2015 | 138 | 4 | 57.93624 | 16170 |
| seda | 1991 | 162 | 4 | 32.18680 | 2000 |
| picape cabine estendida | 2012 | 152 | 4 | 37.01482 | 19299 |
Os dados incluem colunas como estilo do automóvel, ano de fabricação, potência do motor, cilindros, consumo na estrada e valor. Essa empresa não é brasileira, então o valor está em dólar.
Antes de começarmos a rodar alguns modelos, vamos fazer o tratamento dos dados para checar se temos dados nulos. Pois, se tiver teremos que fazer algum tratamento.
Verificando se há informações nulas
Para verificar se temos informações nulas, na célula seguinte escrevemos any(is.na()) passando nos parênteses o dataframe que é dados.
any(is.na(dados))
FALSE
Ao executar, notamos que é falso, ou seja, não temos dados nulo e não será necessário nos preocupar com isso. Mas, tem um detalhe. Como mencionamos anteriormente, essa primeira coluna, que é o estilo do automóvel, é uma coluna que são dados categóricos. Então, tem várias categorias. O carro pode ser sedã, SUV, entre outros. Estamos com um texto e em Modelos de Machine Learning precisam, geralmente, trabalhar apenas com dados numéricos. Ou seja, dependendo do modelo que vamos utilizar, teríamos que transformar essas categorias em números. No nosso caso, os modelos que utilizaremos nas aulas não têm essa necessidade. Podemos trabalhar com categoria de texto, mas vamos ter que converter esse tipo de caractere num tipo chamado fator, que é o factor.
Convertendo de caracter para fator
Então, precisamos fazer essa conversão para que os modelos consigam entender com o que estão lidando e realizar as previsões corretamente. Vamos fazer essa conversão de caractere para fator. Vamos sobrescrever no próprio dataframe de dados passando dados < - dados em sequência, vamos encadear as operações usando um operador muito famoso em R, que é o pipe, que é o símbolo de porcentagem, sinal de maior e porcentagem de novo.
Nesse caso, uma função chamada mutate() para fazer a conversão de tipo de dado. Nos parênteses, passamos a coluna que queremos alterar, que no caso é a Estilo. Adicionamos o sinal de igual, seguido de as.factor() para transformar em fator. Nos parênteses, passamos Estilo. Após, executamos.
dados <- dados %>%
mutate(Estilo = as.factor(Estilo))
Agora podemos verificar se deu tudo certo usando a função glimpse(), que consegue mostrar algumas informações rápidas sobre nossos dados. Nos parenteses, passamos dados e executamos.
glimpse(dados)
Rows: 10,819
Columns: 6
$ Estilo < fct > SUV 4 portas, seda, minivan de passageiros, seda, s…
$ Ano < int > 2005, 2016, 2016, 2015, 1991, 2012, 2016, 1994, 199…
$ Potencia_motor < dbl > 275, 170, 248, 138, 162, 152, 365, 230, 205, 155, 1…
$ Cilindros_motor < dbl > 6, 4, 6, 4, 4, 4, 6, 6, 6, 4, 4, 6, 4, 4, 6, 4, 6, …
$ Consumo_estrada_km < dbl > 28.96812, 61.15492, 45.06152, 57.93624, 32.18680, 3…
$ Valor < int > 29695, 30495, 37650, 16170, 2000, 19299, 42600, 238…
São 10.819 linhas que temos, no total e 6 colunas. Dá para visualizar que o Estilo agora, ao invés de caractere, está como fct, que é o fator. Então, deu tudo certo.
Explorando os dados
Agora, podemos também começar a explorar os dados, entender as estatísticas descritivas para entender qual é a média de cada uma das variáveis, quais são os valores máximos e mínimos. Existe uma função no R que facilita muito esse processo, que é a summary(). Nos parênteses, passamos dados e executamos.
summary(dados)
Estilo Ano Potencia_motor Cilindros_motorseda :2780 Min. :1990 Min. : 55.0 Min. : 3.000
SUV 4 portas :2309 1st Qu.:2006 1st Qu.:169.0 1st Qu.: 4.000
cupe : 854 Median :2014 Median :210.0 Median : 6.000
picape cabine dupla : 681 Mean :2010 Mean :228.1 Mean : 5.379
hatchback 4 portas : 665 3rd Qu.:2016 3rd Qu.:285.0 3rd Qu.: 6.000
picape cabine estendida: 623 Max. :2017 Max. :707.0 Max. :12.000
(Other) :2907
Consumo_estrada_km Valor
Min. :19.31 Min. : 2000
1st Qu.:35.41 1st Qu.:19999
Median :41.84 Median :28410
Mean :42.96 Mean :28609
3rd Qu.:49.89 3rd Qu.:38190
Max. :85.30 Max. :74000
Como retorno temos um mini relatório. Para a coluna que é o Estilo que são dados categóricos, trouxe a quantidade que tem de cada categoria. Então, a categoria que mais está presente é o tipo de carro sedã, com 2.780. Em segundo lugar, a SUV 4 portas, com 2.309 além de valores menores para as outras categorias. A categoria "Outras" vamos verificar futuramente.
Em relação ao ano de fabricação, o carro mais antigo é de 1990 e o mais novo de 2017, sendo a mediana 2014 e a média é de 2010. Em relação à potência do motor, temos uma potência mínima de 55 cavalos, a mediana de 210, a média de 228 e o valor máximo parece bem discrepante, 707 cavalos.
Em relação aos cilindros do motor, temos os cilindros indo de 3 a 12, com a mediana de 6 cilindros. Em relação ao consumo na estrada, de quanto faz em quilômetros por litro, temos como mínimo 19,31. A mediana e a média estão em torno de 42 e o valor máximo é 85,30.
O valor mínimo é de 2 mil dólares, tanto a média quanto a mediana estão em torno de 28 mil dólares, e o valor máximo de 74 mil dólares. Conseguimos obter bastante informação sobre essas colunas.
Iniciamos carregando os dados, verificamos se havia alguma informação nula e transformamos caracteres em fatores para utilizar em nossos modelos posteriormente. Também já visualizamos algumas informações importantes.
Próximos passos
Nosso próximo objetivo é entender como essas variáveis estão relacionadas ao valor. O que influencia um carro a ser mais barato ou mais caro? Como isso está ocorrendo? Qual é a correlação entre essas variáveis e o valor? Vamos explorar isso no próximo vídeo. Esperamos você lá.
Regressão linear múltipla - Analisando a relação entre as variáveis
Carregamos os dados e agora chegou o momento de entender qual é a relação de cada uma dessas variáveis que temos com o valor dos automóveis. Será que a gente tem uma relação linear, ou seja, conforme o valor da variável aumenta, o valor do automóvel também aumenta? É isso que a gente vai descobrir agora. Vamos entender como essas variáveis influenciam o valor dos automóveis.
Para isso, podemos criar alguns gráficos para cada uma das variáveis para entender essas relações. Se considerarmos o estilo do automóvel, que é a primeira variável, temos as categorias. Será que tem algum estilo que é mais caro que outro? Como que isso acontece?
Podemos criar, por exemplo, um gráfico de colunas que mostre a média de valor por estilo, obtendo insights a partir disso. Então, vamos criar alguns gráficos, começando pelo estilo.
Criando gráfico de estilo
Antes de começar, podemos definir as configurações da largura e altura dos gráficos para termos uma boa visualização. Então, digitamos options(repr.plot). Primeiro, definiremos a largura, então escrevemos width = 10. Adicionamos vírgula e definimos a altura repr.plot.height = 6 e executamos.
options(repr.plot.width = 10, repr.plot.height = 6)
Se queremos criar primeiro um gráfico de colunas do estilo com a média do valor, precisamos chamar nossos dados. Precisamos agrupar esses automóveis conforme o estilo. Então, usaremos o operador pipe dados %>%. Na linha abaixo, usaremos a função group_by(). Nos parênteses, passamos Estilo e fora passamos o pipe novamente %>%.
Agrupamos por estilo, mas queremos a média de valor pra cada categoria que temos. Usaremos uma função chamada summarise(). Nos parênteses, criamos a variável media_Valor. Adicionamos o sinal de igual e passamos a média, que é mean(). Para essa função, passamos a coluna Valor, para obter essas médias. Na mesma linha, passamos %>%.
Abaixo, criaremos o gráfico chamando ggplot(). Nos parênteses, chamamos aes() para definir os eixos, então passamos x = Estilo. Inclusive, podemos pedir pra ordenar da maior média pra menor, pra ter um gráfico mais fácil de visualizar e conseguir obter algum insight.
Para fazermos essa ordenação, antes do Estilo, passamos o reorder(), envolvendo o Estilo e também passando a media_valor. Adicionamos vírgula e definimos y = media_valor.
Fora dos parênteses, na mesma linha, adicionamos o sinal de +, na linha seguinte, definiremos o tipo de gráfico que criaremos, nesse caso o de colunas. Escrevemos geom_col() + e pulamos para a próxima linha.
Também podemos pedir pra deixar esse gráfico com as colunas na horizontal pra ficar mais fácil de visualizar. Para isso, escrevemos coord_flip() +, para que rotacione.
Na linha abaixo, definiremos os rótulos dos eixos passando labs(). Começaremos com o título, então, nos parênteses escrevemos title = ''Média do valor por estilo do automóvel. Adicionamos vírgula e passamos o rótulo do eixo x vazio, x = ''. Entenderemos o motivo disso depois.
Na linha abaixo, passamos y = 'Média do valor'. Por fim, para o gráfico ficar bem completo, podemos colocar um tema para conseguir modificar algo, como o tamanho da fonte. Porque o tamanho da fonte vai ficar pequeno, se quisermos um pouco maior, podemos alterar da seguinte forma. Na última linha, passamos theme(text = element_text(size = 16)).
dados %>%
group_by(Estilo) %>%
summarise(media_valor = mean(Valor)) %>%
ggplot(aes(x = reorder(Estilo, media_valor), y = media_valor)) +
geom_col() +
coord_flip() +
labs(title = 'Média do valor por estilo do automóvel',
x = '',
y = 'Média do valor') +
theme(text = element_text(size = 16))
Após executar, temos o seguinte gráfico.
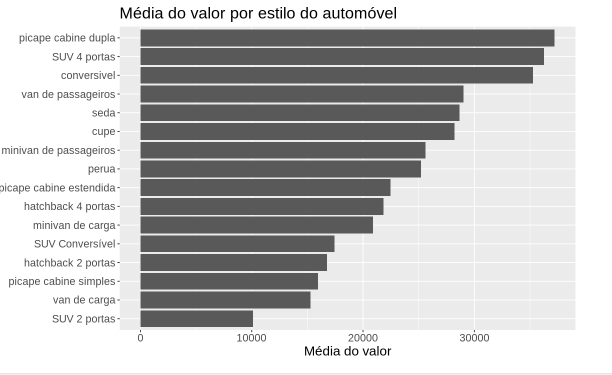
Temos a média do valor por estilo do automóvel. Como média de maior valor temos a picape de cabine dupla, seguido do SUV 4 portas, conversível e outros. Já automóveis com valores mais baixos temos Hatchback 2 portas, picape cabine simples, Van de carga e SUV 2 portas. Então, a partir desse gráfico, conseguimos entender que sim, o estilo do automóvel tem uma influência em relação ao ao valor dele.
Avaliando o impacto do ano do automóvel no valor
Agora, vamos seguir para a próxima variável, o ano. Vamos descobrir se quanto mais velho o automóvel, mais barato é. Para isso, escrevemos ggplot(dados, aes(x = Ano, y = Valor)). Usaremos o gráfico de pontos. Adicionamos o sinal de + e na próxima linha chamamos geom_point() e executamos.
ggplot(dados, aes(x = Ano, y = Valor)) +
geom_point()
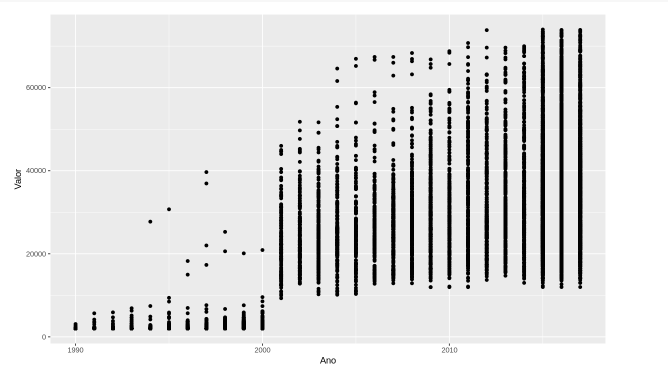
Conseguimos notar que até o ano 2000 temos valores mais baixos, especialmente nos primeiros anos. Quando chega próximo de 2000, temos valores que estão mais dispersos. Há automóveis que são mais antigos, mas tem valor de 20 mil, 40 mil dólares.
Então, mesmo que no começo tenha valores baixos e dispersões nos anos seguintes, os valores aumentam ao longo do tempo, mas não há uma relação linear.
Investigando a relação entre potência do motor e valor
Sabendo disso, vamos checar a próxima variável. Para isso, copiamos o mesmo código da célula acima e colamos na nova célula. Agora, faremos as alterações necessárias. Mudamos o valor de X para Potencia_motor e executamos a célula.
ggplot(dados, aes(x = Potencia_motor, y = Valor)) +
geom_point()
Assim, temos um resultado diferente, com uma concentração em alguns pontos, seguindo o que parece algo linear. Conforme a potência vai aumentando, o valor também aumenta, embora tenhamos alguns pontos que não estejam tão nesse padrão. Além disso, quando temos a potência do moto alta, acima de 600, há valores que não estão seguindo a reta. Para facilitar nossa visualização, vamos adicionar essa reta.
Para isso, após geom_point() adicionamos + e pulamos para a próxima linha. Nela, escrevemos geom_smooth(method = 'lm'), passando o linear model que vai ajustar uma linha de tendência como se fosse um modelo de regressão linear. Adicionamos vírgula e passamos outros parâmetros, como se = FALSE, que adiciona uma linha de um intervalo de confiança na reta, mas a gente não precisa disso nesse momento. Em seguida, adicionamos color = 'red' e executamos.
ggplot(dados, aes(x = Potencia_motor, y = Valor)) +
geom_point() +
geom_smooth(method = 'lm', se = FALSE, color = 'red')
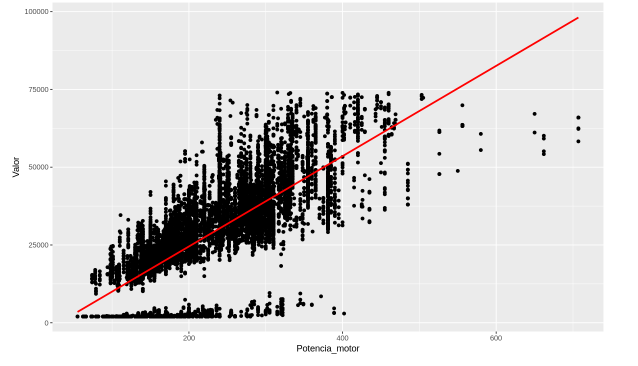
Temos a linha de tendência em vermelho e conseguimos visualizar tudo o que mencionamos anteriormente. Vários dados estão dentro dessa linha, mas temos informações que estão para fora, que são os valores mais altos da potência do motor. Então, temos uma relação que é linear, mas ainda tem alguma dispersão.
Examinando o número de cilindros do motor
Vamos analisar as outras variáveis. Para isso, copiamos a mesma célula anterior. Mudamos o valor de X para Cilindros_motor e executamos.
gplot(dados, aes(x = Cilindros_motor, y = Valor)) +
geom_point()
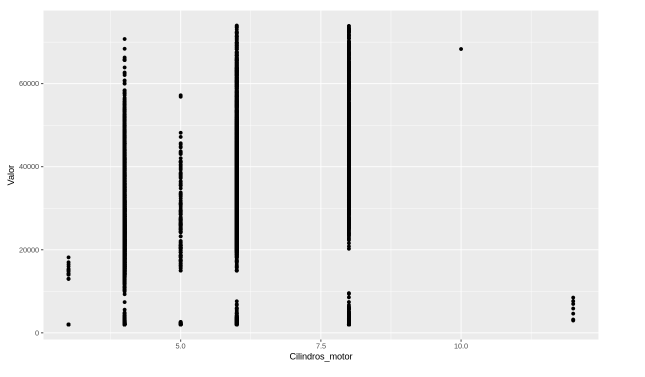
Lembrando que os cilindros iam de 3 até 12 e não tínhamos um padrão em que conseguíamos identificar a linearidade. Agora, quando há um número menor de cilindros, os dados estão com um valor menor, indo até 20 mil dólares. Já quando o cilindro aumenta um pouco o valor também, depois cai. Não temos um padrão em que consigamos extrair algo linear.
Analisando o consumo na estrada e o valor do automóvel
Vamos checar como está a questão do consumo lá na estrada, de quilômetros por litro. Novamente, copiamos o mesmo código e mudamos o valor de x por Consumo_estrada_km.
ggplot(dados, aes(x = Consumo_estrada_km, y = Valor)) +
geom_point()
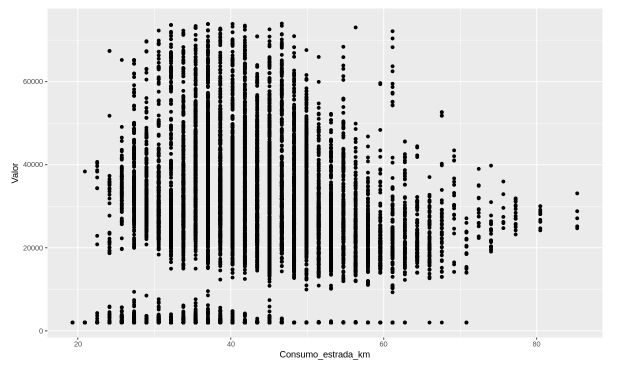
Também temos um padrão que não está seguindo uma linearidade, tem muita dispersão. Inclusive, no final, com o consumo na estrada mais elevado, temos valores mais baixos. Porém, não encontramos um padrão.
Conseguimos analisar tudo isso com gráficos. Agora, podemos aplicar outra técnica, que é analisar a correlação entre essas variáveis para entender como realmente está a associação de cada uma com o valor, pra entender qual está influenciando mais no valor dos automóveis.
Analisando a correlação entre as variáveis
Primeiro, podemos separar só as colunas numéricas. Para isso, criamos a variável dados_numericos <- dados %>% seguido da função select_if(is.numeric), assim, se for numérico, vamos selecionar. Após, criamos a matriz de correlação matriz_correlacao <- cor(dados_numericos). Por fim, chamamos matriz_correlacao e executamos.
dados_numericos <- dados %>% select_if(is.numeric)
matriz_correlacao <- cor(dados_numericos)
matriz_correlacao
| Ano | Potencia_motor | Cilindros_motor | Consumo_estrada_km | Valor | |
|---|---|---|---|---|---|
| Ano | 1.0000000 | 0.3890908 | -0.1065934 | 0.3577647 | 0.6966555 |
| Potencia_motor | 0.3890908 | 1.0000000 | 0.6952144 | -0.43319516 | 0.7361250 |
| Cilindros_motor | -0.1065934 | 0.6952144 | 1.0000000 | -0.70162167 | 0.3040547 |
| Consumo_estrada_km | 0.3577647 | -0.43319516 | -0.70162167 | 1.0000000 | -0.0475750 |
| Valor | 0.6966555 | 0.7361250 | 0.3040547 | -0.0475750 | 1.0000000 |
Temos esse resultado contendo cada uma das variáveis versus ela mesma. Só que nosso foco será na última linha dessa matriz, a do valor. Vamos comparar a correlação do valor com o ano, que é de 0,70, alta e positiva. Isso indica que quanto maior o ano, maior será o valor do automóvel.
Depois, temos a potência do motor, que tem uma correlação de aproximadamente 0,74, positiva e alta também. Ou seja, quanto maior a potência, maior o valor do automóvel.
Nos cilindros do motor a correlação é positiva, mas baixa. Possui 0,30, ou seja, isso influência muito menos que variáveis como o ano e a potência do motor. Por fim, tem o consumo na estrada em quilômetros por litro, que é de menos 0,04, ou seja, quase nulo. Isso significa que a variável não está influenciando em relação ao valor do automóvel.
Conseguimos extrair muitos insights e entender quais variáveis estão mais associadas e influenciam no preço do automóvel. No próximo vídeo, começaremos a criar nosso primeiro modelo para fazer as previsões dos valores. Bora lá?
Sobre o curso Estatísticas com R: testando modelos de regressão
O curso Estatísticas com R: testando modelos de regressão possui 177 minutos de vídeos, em um total de 51 atividades. Gostou? Conheça nossos outros cursos de Estatística em Data Science, ou leia nossos artigos de Data Science.
Matricule-se e comece a estudar com a gente hoje! Conheça outros tópicos abordados durante o curso:
- Regressão linear múltipla
- Árvore de decisão
- Técnicas de Ensemble
- Técnica de Boosting
- Comparando modelos e utilizando novos dados