Keras: primeiros passos em redes neurais
O neurônio - Apresentação
Olá! Eu me chamo Mirla Borges, sou instrutora da Alura e te acompanharei no curso de Redes Neurais com Keras.
Mirla é uma mulher branca e jovem de cabelos chacheados e pretos na altura dos ombros. Seus olhos são castanhos e ela usa óculos de grau com armação redonda. Mirla também usa um piercing de argola prata no nariz (septo) e aparelho ortodôntico. Está vestida com uma regata preta e suas unhas pintadas em tom de cinza. Ao fundo, há uma parede verde.
Esse curso é para quem tem interesse em aprender sobre redes neurais e em construí-las utilizando a API do Keras. Para isso, vamos modelar uma MLP para classificar flores. Chegaremos ao final do curso compreendendo:
O funcionamento de uma rede neural
Como construir um modelo neural de várias camadas com Keras
Como avaliar o desempenho da rede neural após o treinamento
Para um maior aproveitamento dos conteúdos, é interessante que você tenha alguns conhecimentos em Python e também da biblioteca Matplotlib, Pandas e Sklearn. Vamos lá?!
O neurônio - Neurônio biológico
Durante o projeto do nosso curso, vamos entender e explorar um banco de dados de flores. Esse banco tem como entrada quatro características:
Comprimento e largura de pétalas
Comprimento e largura de sépalas
Nós vamos verificar e classificar, de acordo com essas entradas, se a flor Iris é do tipo:
Versicolor
Setosa
Virginica
Essas são as três classificações. Resolveremos esse problema das multi classes, utilizando Redes Neurais. Nosso objetivo é construir uma rede neural capaz de classificar o nosso dataset Iris. Eu disponibilizei um Notebook que você pode usar para acompanhar o curso. Ele tem vários textos informativos que serão úteis no processo de construção do código para o nosso modelo neural.
Este Note conta com a representação das nossas folhas, detalhando qual é a área da pétala e da sépala na nossa Iris. A sépala fica mais abaixo e é maior, enquanto a pétala é menor e fica na parte de cima.
Além disso, temos três tipos de flores/Iris: setosa, versicolor e virginica, também com a descrição de onde está a pétala e a sépala. Talvez você esteja se perguntando o motivo de usarmos uma rede neural, sendo que existem vários tipos de modelos de machine learning disponíveis.
Redes Neurais é um subcujunto dentro do grande conjunto de Machine Learning
Nesse conjunto, nós encontraremos outros modelos, como o Support Vector Machine, as Árvores de Decisão, dentre outros.
As redes neurais conseguem ter perfomance melhor que modelos tradicionais em problemas complexos
Por isso, elas são muito utilizadas em:
Carros autônomos
Problemas que envolvem tratamento de imagem, áudio e vídeo
As redes neurais são muito potentes, suas construções são únicas e utilizam funções que as otimizam, por isso, vamos aprender a construir uma rede neural e solucionar nosso problema do Iris Dataset com o modelo neural.
Antes de construirmos nosso projeto, precisamos entender o que é uma rede neural.
O que é uma Rede Neural
Para aprender o que é uma Rede Neural, vamos nos guiar pela História. As redes neurais não foram inventadas agora, os estudos nessa área acontecem há anos. Quero te contar a história das redes neurais, porque ela é inspiradora e envolve muito estudo, dedicação e pesquisa.
Começando pela História
A história das redes neurais começa em 1943, quando Warren McCulloch e Walter Pitts publicaram o primeiro artigo descrevendo como o neurônio funciona em uma arquitetura. Neste caso, como o neurônio poderia ser descrito?
Funcionamento de um neurônio
Basicamente, um neurônio é constituído por quatro partes principais: Dendritos; Corpo celular; Axônio; e os Terminais sinápticos
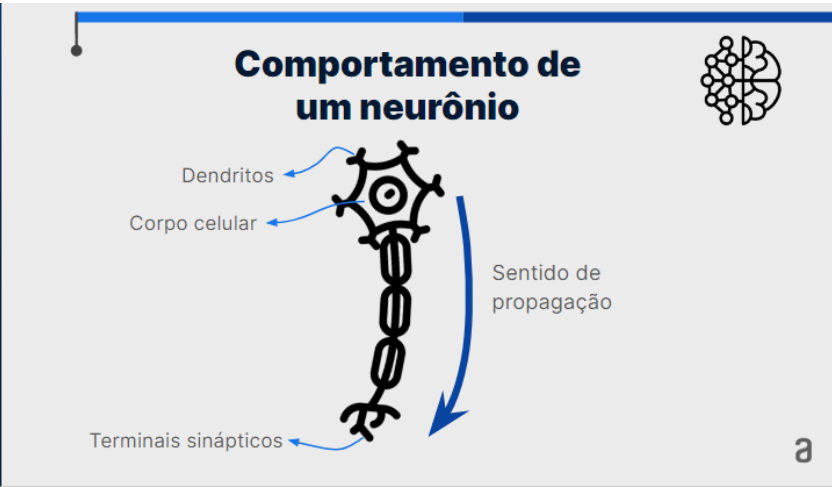
Cada uma dessas quatro partes tem uma função. Nós vamos conversar sobre os "Dendritos", o "Corpo Celular" e os "Terminais sinápticos". Um ponto interessante é que o sentido de propagação da informação, isto é, de um impulso elétrico que chega ao neurônio se dá dos dendritos até os terminais sinápticos.
- Dendritos
Os dendritos são como uma porta que recebe a informação. Essa informação são os sinais sinápticos que chegam nos dendritos, que estão na extremidade.
- Corpo celular
Depois, os sinais são enviados ao corpo celular, que processará os sinais considerando a função do neurônio.
Por exemplo, se os neurônios são responsáveis pelo toque, quando pegamos uma caneta e tocamos a bochecha, os neurônios processarão essa pressão na bochecha. É um toque que, provavelmente, não oferece riscos. Enfim, os neurônios localizam e entendem que é só um toque.
O mesmo se aplica ao paladar e o reconhecimento de alimentos doces, salgados. Essa é a função do corpo celular: processar os sinais recebidos. A informação passa pelo axônio e chega aos terminais sinápticos.
- Terminais sinápticos
Nos terminais sinápticos, o sinal é enviado para outros neurônios. É onde acontece a comunicação com os demais neurônios.
Agora já sabemos como um neurônio funciona. Como os nossos protagonistas criaram uma arquitetura baseada no neurônio?
Quando Wharren e Walter estavam estudando, os computadores não eram tão difusos, a segunda guerra ainda não havia terminado e eles não tinham acesso a computadores. Então, esses pesquisadores construíram uma arquitetura eletrônica, isto é, com base em componentes eletrônicos e assim surgiu, por exemplo, a porta lógica AND.
A porta AND tem entradas, que podem ser X1 ou X2. É nas entradas que ela vai receber o impulso elétrico. Podemos compará-las aos dendritos, que é onde o neurônio recebe os sinais sinápticos. Depois, esses sinais são enviados para uma função que realizará o processamento, da mesma forma que acontece com o corpo celular.
A diferença é que, na porta AND, a função pode ter dois tipos de saídas, isto é, duas classes de saída que, no nosso exemplo, foram nomeadas de classe 〇 (bola) e classe X.
Esse processamento resultará em um desses dois valores e na saída, que é a terceira e última parte da porta AND. Podemos comparar a saída ao Terminal sináptico, local de saída da nossa porta lógica.
Para entendermos melhor essa porta lógica, vamos usar uma tabela chamada Tabela Verdade. Nela, os valores de X1, isto é, as entradas, podem ser valores binários, 0 e 1, e apenas quando há duas entradas do valor 1, o valor de saída é X.
| 1 | 〇 | X |
|---|---|---|
| 0 | 〇 | 〇 |
| 0 | 1 |
| X1 | X2 | Y |
|---|---|---|
| 0 | 0 | 〇 |
| 0 | 1 | 〇 |
| 1 | 0 | 〇 |
| 1 | 1 | X |
Assim, entendemos o funcionamento do neurônio artificial/eletrônico executado por Wharren e Walter.
O neurônio - Neurônio artificial
Vamos voltar ao nosso problema de classificação: a flor Iris. Nós temos três tipos de classes e há uma espécie dessa flor que vai ser um desses tipos, a depender do tamanho de suas pétalas e sépalas.
Podemos considerar a existência de dois tipos de flores/espécies, a do tipo 1 e a do tipo 2. As flores do tipo 1 têm sépalas mais espessas e maiores, principalmente se compararmos com as flores do tipo 2, que têm pétalas mais finas e menores.
Se classificarmos essas flores com base na largura e no comprimento, teremos dois conjuntos de dados. Esses conjuntos serão representados com desenhos das flores dentro de um retângulo.
O primeiro conjunto está mais concentrado na origem do plano cartesiano (vértice inferior esquerdo do retângulo) e corresponde às flores do tipo 2, com pétalas menores e pequenas;
O segundo conjunto ficará mais distante da origem (próximo ao vértice superior direito do retângulo) e corresponde às flores do tipo 1, com flores maiores e mais espessas.
A partir disso, surge a questão: como ensinar uma máquina a dizer se uma flor é do tipo 1 ou do tipo 2? Como uma máquina pode saber separar esses dois conjuntos?
A resposta é que a máquina parte da ideia de que temos um problema linearmente separável. Se ele é linearmente separável, podemos traçar uma reta diagonal que separa esses dois conjuntos dentro do retângulo. Tudo que está acima da reta são flores do tipo 1.
Portanto, se eu tiver uma flor com largura e comprimento acima da reta, significa que ela é uma flor do tipo 1. Por consequência, tudo que estiver abaixo da reta são flores do tipo 2. Essa divisão está completamente correta. Podemos até fazer um comparativo com o que conhecemos sobre a lógica AND.
| 1 | 〇 | X |
|---|---|---|
| 0 | 〇 | 〇 |
| 0 | 1 |
O X é o único que vai aparecer apenas quando tivermos o resultado 1 e 1 nas entradas. Sendo assim, conseguimos dividir as categorias com uma reta diagonal que separa a classe X da classe 〇 (bola). A ideia é construir um modelo que faça a máquina criar a reta de separação e resolva o problema de classificação.
Retomando a História
O problema de classificação foi solucionado por Frank Rosenblatt que, em 1957, desenvolveu a arquitetura computacional Perceptron. A Perceptron consegue simular um neurônio biológico e dividir as classes. Por conta desta criação, Frank é considerado pai do deep learning.
Perceptron: unidade básica da rede neural
O perceptron é a unidade básica da construção de uma rede neural. Todos os estudos que envolveram redes neurais ao longo dos anos tiveram como origem o desenvolvimento do Perceptron. Também podemos dizer que o Perceptron é um modelo neural que associa pesos às entradas e vamos conseguir compreender melhor o que isso significa explorando suas partes.
O neurônio artificial é dividido em cinco partes.
Parte 1: entradas. Vamos nomeá-las como X1, X2...Xn, sendo n qualquer quantidade. O modelo pode ter 3, 2, 40, 50 entradas, enfim, qualquer valor, e essas entradas precisam corresponder às características do conjunto de dados, isto é, à quantidade de colunas do conjunto de dados
Parte 2: pesos. Nessa camada temos os pesos W1 e W2 até Wn. A quantidade de pesos é correspondente à quantidade de entradas, então, no caso de três entradas, teremos três pesos, quatro entradas, quatro pesos e assim por diante.
Ainda na segunda parte, um ponto importante é o b*, isto é, o *bias ou viés. O b serve para adicionar um novo viés ao cálculo do modelo. Ele permite que ocorra a construção da reta de separação.
Parte 3: soma. A função soma vai executar a ponderação dos pesos com as entradas, até porque os pesos têm a missão de ponderar as entradas.
Parte 4: ativação. A função de ativação recebe os dados da soma e gera uma saída.
Parte 5: saída. Nós chamamos a saída de y e, normalmente, ela é a classificação. Então, será uma flor do tipo 1, de pétalas maiores ou uma flor do tipo 2, de pétalas mais finas.
O sentido de propagação da informação é sempre das entradas para a saída. Este sentido se assemelha ao de um neurônio biológico. O aprendizado não se dá de qualquer maneira. Ele acontece nas camadas de soma e ativação.
O aprendizado de um perceptron passa, primeiro, pela função soma. A função soma é, basicamente, um cálculo matemático de soma ponderada dos pesos pelas entradas. Como temos o valor de bias, também o adicionamos nessa equação.
O resultado da soma dos pesos com as entradas será enviado para a nossa função de ativação. Ela retornará um resultado correspondente à saída y. Esse resultado depende muito do tipo de função de ativação utilizada. Essas duas funções, soma e ativação, são muito importantes para o processo de aprendizagem.
Quando a criação é feita, há uma verificação se os valores dos pesos correspondem ou não corretamente com a reta de separação. Mas, como isso é feito? Vamos supor que criamos o Perceptron e ele receberá a largura e o comprimento da flor. Existirá um peso para a largura e para o comprimento, além do valor de bias, que é o nosso viés.
Nós utilizaremos uma equação da reta e realizaremos algumas atividades onde ela será explicada. Por isso, não deixe de ler e fazer as atividades, pois, com elas, compreenderemos como essa equação está associando as entradas e pesos a um valor para a reta.
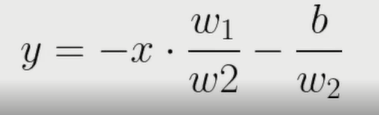
Os valores de w1, w2 e b, correspondentes aos pesos, são alterados constantemente dentro do aprendizado. Supondo que iniciamos nosso Perceptron com valores aleatórios de pesos, por exemplo: w1 -3; w2 = 4; e b = 1. A reta de separação se dará da seguinte maneira:
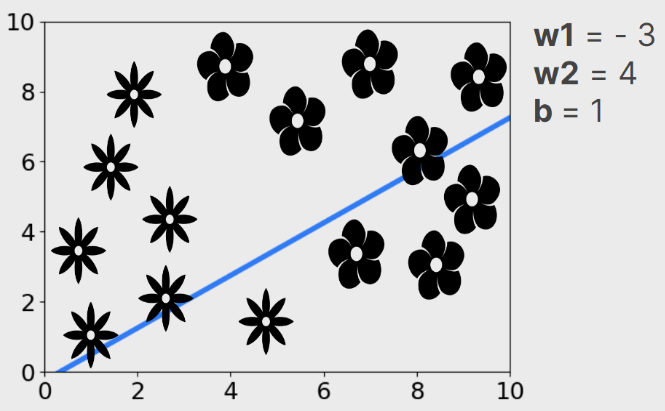
O foco da reta está na origem e ela está inclinada de tal forma que não conseguirá separar os conjuntos, isto é, as flores. Não é possível dizer que acima da reta temos um conjunto do tipo 1 e, abaixo da reta, um conjunto do tipo 2. Ela não separa nada, portanto, não é útil.
O modelo Perceptron vai entender que os valores não estão corretos para w1, w2 e b, e vai atualizar os pesos até o momento em que teremos um bom resultado, ou seja, que separe corretamente o problema. No caso, um resultado em que: w1 = 4; w2 = 2; e b = - 28.
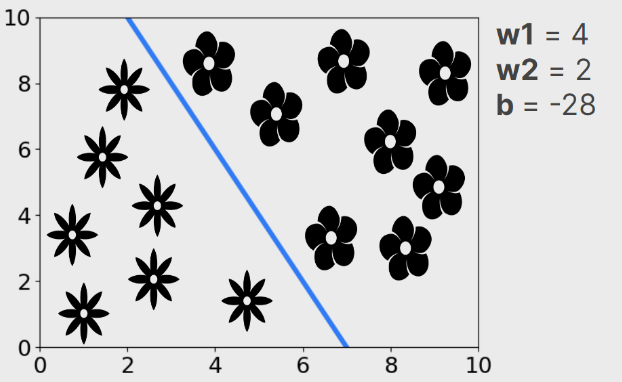
Com isso, uma reta foi gerada e ela consegue separar corretamente os dois conjuntos de dados. Desta maneira, é possível solucionar o problema de classificação, pois para qualquer valor inserido para a flor, nós encontraremos o tipo correto de flor.
Sobre o curso Keras: primeiros passos em redes neurais
O curso Keras: primeiros passos em redes neurais possui 146 minutos de vídeos, em um total de 51 atividades. Gostou? Conheça nossos outros cursos de Machine Learning em Data Science, ou leia nossos artigos de Data Science.
Matricule-se e comece a estudar com a gente hoje! Conheça outros tópicos abordados durante o curso:
- O neurônio
- Multi-layer Perceptron
- Dados de flores
- Modelo neural
- Avaliação do modelo