Machine Learning parte 2: otimização com exploração aleatória

Randomized Search e Cross validation combinadas - Introdução

No curso anterior sobre otimização de estimadores por meio de hiperparâmetros, estávamos, em um grid, discretizando o espaço de hiperparâmetros e buscando, de maneira exaustiva, os melhores resultados.

Por exemplo: quando nosso estimador tinha duas dimensões (max_depth e min_samples_leaf), nós testávamos diversos valores diferentes em sequência, abordando todo aquele espaço de parâmetros no grid.

Feito isso, decidíamos explorar de maneira mais refinada determinados espaços... e assim sucessivamente. Porém, esse processo consome muito tempo e processamento computacional, o que certamente resultaria em custos financeiros.

Se tínhamos esse problema com duas dimensões, imagine se tivéssemos três dimensões, ou quatro... ou uma quantidade ainda maior de parâmetros? O número de combinações gerado seria gigantesco, e levaria muito tempo para chegarmos a um resultado.

Existem outras maneiras de buscarmos a melhor otimização para nossos estimadores. Por exemplo, ao invés de explorarmos exaustivamente o espaço de parâmetros (ou um subespaço discretizado), colocaremos nossos hiperparâmetros em um grid (não necessariamente de maneira discreta, mas também de maneira contínua), e testaremos valores aleatórios.

A ideia é que não existe a necessidade de explorar todo o espaço de parâmetros para encontrar pontos de mínimo ou de máximo que sejam bons o suficiente para o problema que estivermos tentando resolver - não necessariamente o mínimo global ou o máximo global, mas valores que sejam suficientemente adequados para a situação problema.

Ou seja, enquanto a busca no grid (grid search) vai varrer todas as possibilidades e demora muito tempo, apesar de ser possível rodá-lo de maneira paralela, a busca aleatória (random search) vai rodar em menos tempo e permite outras otimizações, pois não iremos explorar exaustivamente todos os valores possíveis do nosso espaço de hiperparâmetros.

Nesse curso, aprenderemos como implementar uma busca aleatória e como preparar as soluções a partir disso. Assim como no curso anterior, na maior parte do processo trabalharemos com a validação cruzada.

Porém, em determinado ponto, também abordaremos, com o auxílio do train_test_split, a otimização de hiperparâmetros sem validação cruzada, mantendo as fases de treino, teste e validação.

Dessa forma, você terá as duas opções para utilizar no seu dia-a-dia. Vamos começar?

Randomized Search e Cross validation combinadas - Explorando aleatoriamente

Já aprendemos que, quando temos um espaço de parâmetros com duas dimensões, podemos explorá-lo ponto a ponto. Isto é, transformamos espaços contínuos em espaços discretos e exploramos, nesses pontos, o nosso algorítimo.

Por exemplo, se estamos trabalhando com um algorítimo de DecisionTreeClassifier que tem os parâmetros max_depth e min_samples_leaf, podemos testar cada um desses parâmetros com um valor específico. Depois de medirmos o resultado, repetimos o processo para o próximo parâmetro.

Dessa forma, exploramos o espaço até completarmos o grid todo. Por exemplo, se temos 15 condições para cada parâmetro, rodamos o algorítimo 225 vezes para explorar esse espaço por completo.

Mas e quando temos 3 parâmetros, cada um com uma determinada quantidade de condições? Nesse caso, ainda poderíamos plotar esses dados em um gráfico 3D... mas e se tivéssemos 4 parâmetros ou mais?

Supondo que tivéssemos 3 parâmetros com 64 condições cada um, e um parâmetro com apenas 2 condições. Nessa situação, teríamos que explorar 524.288 possibilidades de parâmetros. Se cada uma dessas explorações levasse 5 minutos (o que é um exemplo razoável), seriam necessários 1820 dias para testar todas essas possibilidades. Se estivéssemos rodando esse algorítimo em 5 máquinas, ainda assim levaríamos 1 ano para terminar o processo.

Vamos analisar o grid de duas dimensões abaixo:

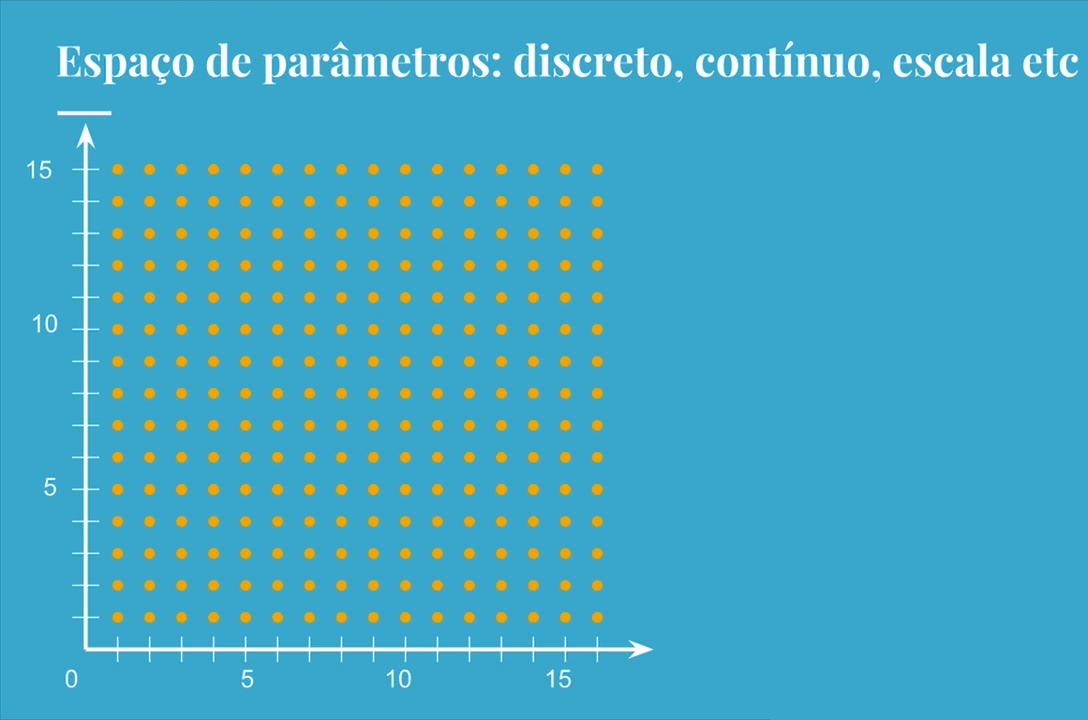
Mesmo que não haja garantia disso, esperamos que os valores representados no grid tenham resultados próximos aos seus vizinhos. Ou seja, pode não existir uma mudança brusca entre pontos muito próximos do nosso espaço discretizado de parâmetros.

Com isso em mente, ao invés de tentarmos explorar todo o grid (o que é feito no grid search), poderíamos buscar pontos aleatoriamente (random search). E é exatamente isso que faremos agora.

Começaremos essa busca aleatória ao final do projeto no qual trabalhamos no curso anterior. Se você não fez o curso, pode fazer o download do projeto neste link ou visualizar os arquivos no GitHub.

Para organizarmos nosso trabalho, adicionaremos uma célula de texto indicando onde se inicia o RandomSearch. Esse processo de busca é bastante parecido com tudo o que fizemos anteriormente, e também se inicia definindo um espaço de parâmetros a ser explorado.

Portanto, começaremos copiando o código que criamos para GridSearchCV:

from sklearn.model_selection import GridSearchCV, KFold

SEED=301
np.random.seed(SEED)

espaco_de_parametros = {
    "max_depth" : [3, 5],
    "min_samples_split": [32, 64, 128],
    "min_samples_leaf": [32, 64, 128],
    "criterion": ["gini", "entropy"]
    
}

busca = GridSearchCV(DecisionTreeClassifier(),
                    espaco_de_parametros,
                    cv = KFold(n_splits = 5, shuffle=True))

busca.fit(x_azar, y_azar)
resultados = pd.DataFrame(busca.cv_results_)
resultados.head()

Em seguida, alteraremos os campos em que GridSearchCV aparece para RandomizedSearchCV. Manteremos a mesma SEED e o mesmo espaço de parâmetros (com 36 possibilidades). Quando trabalhos com processos aleatórios, é muito comum que o modelo contenha um parâmetro random_state para manter a consistência entre todas as execuções. No caso, esse parâmetro receberá nosso SEED como valor.

Dentre essas 36 possibilidades de combinações de parâmetros, quantas queremos rodar? Se executarmos todas, estaremos fazendo exatamente a mesma busca que com o GridSearchCV, alterando apenas a ordem. Ou seja, devemos executar somente algumas.

Um dos parâmetros que RandomizedSearchCV pode receber é o número de iterações - n_iter. A ideia é, nesse momento, rodarmos apenas 16 dessas possibilidades:

from sklearn.model_selection import RandomizedSearchCV

SEED=301
np.random.seed(SEED)

espaco_de_parametros = {
    "max_depth" : [3, 5],
    "min_samples_split": [32, 64, 128],
    "min_samples_leaf": [32, 64, 128],
    "criterion": ["gini", "entropy"]
    
}

busca = RandomizedSearchCV(DecisionTreeClassifier(),
                    espaco_de_parametros, 
                    n_iter = 16,
                    cv = KFold(n_splits = 5),
                          random_state = SEED)


busca.fit(x_azar, y_azar,groups = dados.modelo)
resultados = pd.DataFrame(busca.cv_results_)
resultados.head()

Após a execução desse código, queremos saber quão bem se saiu o melhor classificador. Da mesma forma que no GridSearchCV, encontraremos uma resposta com cross_val_score() (nested cross validation).

from sklearn.model_selection import cross_val_score

scores = cross_val_score(busca, x_azar, y_azar, cv = KFold(n_splits=5, shuffle=True))
scores

O resultado na tela será um array de cinco valores:

array([0.7755, 0.78 , 0.8055, 0.7855, 0.774 ])

Também iremos imprimir a acurácia média dessas cinco amostras e o intervalo que obtivemos:

from sklearn.model_selection import cross_val_score

scores = cross_val_score(busca, x_azar, y_azar, cv = KFold(n_splits=5, shuffle=True))
imprime_score(scores)

Accuracy médio 78.69

Intervalo [76.70, 80.68]

Em seguida, para encontrarmos o melhor estimador, atribuiremos a função busca.best_estimator_ à uma variável melhor e imprimiremos essa variável na tela.

DecisionTreeClassifier(class_weight=None, criterion='gini', max_depth=5,
            max_features=None, max_leaf_nodes=None,
            min_impurity_decrease=0.0, min_impurity_split=None,
            min_samples_leaf=128, min_samples_split=128,
            min_weight_fraction_leaf=0.0, presort=False, random_state=None,
            splitter='best')

Nota sobre o valor atribuído ao parâmetro do max_depth aqui ser = 5 ser diferente do = 3 que o instrutor apresenta na aula. Isto foi colacado para te ajudar a exercitar e entender com uma pouco mais desta propriedade e podermos enfatizar com vc que ao definir o parâmetro "max_depth", você está limitando a quantidade de camadas que a árvore de decisão pode ter e junto a isso podermos adicionalmente te informar que:

• Se você definir um valor baixo para "max_depth", a árvore será mais rasa, terá menos nós de divisão e menos perguntas sobre os atributos dos dados. Isso pode levar a um modelo mais simples, mas também pode reduzir a capacidade de capturar relações complexas nos dados.

• Por outro lado, se você definir um valor alto para "max_depth", a árvore poderá se tornar mais profunda, ter mais nós de divisão e realizar mais perguntas sobre os atributos dos dados. Isso pode resultar em um modelo mais complexo, capaz de capturar relações mais detalhadas nos dados de treinamento, mas também pode aumentar o risco de overfitting.

• É importante ajustar adequadamente o valor de "max_depth" com base na natureza do problema, no tamanho do conjunto de dados e em outras considerações específicas do modelo, como o número de recursos disponíveis. Um ajuste cuidadoso desse parâmetro pode ajudar a obter um equilíbrio entre o viés e a variância do modelo, melhorando sua capacidade de generalização.**

Agora voltando o nosso raciocínio ao que é demonstrado na sequência em nossa prática desta curso....

Isso significa que o melhor estimador teve o critério gini, a profundidade máxima 5, o mínimo de elementos na folha 128 e, e 128 como o mínimo de splits antes de tomar uma decisão. Tivemos uma acurácia média de 78.69%, em um intervalo entre 76.70% e 80.68%.

Repare que executando menos da metade das buscas, obtivemos uma acurácia média e um intervalo muito parecidos com aqueles do GridSearchCV (que tinha a média 78.68% e o intervalo 76.85% a 80.55).

Nesse ponto, também podemos gerar a árvore de decisões:

features = x_azar.columns
dot_data = export_graphviz(melhor, out_file=None, filled=True, rounded=True,
                        class_names=["não", "sim"],
                        feature_names = features)

graph = graphviz.Source(dot_data)
graph

Como a árvore é bem grande, mostraremos somente parte dela nessa página:

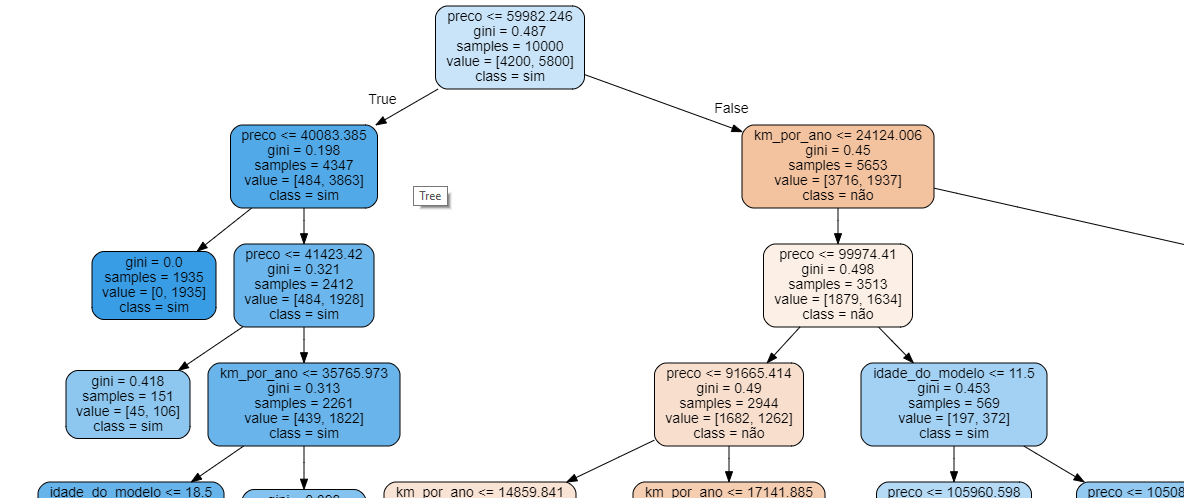
Na prática, a utilização do RandomizedSearchCV nos permite encontrar valores muito próximos aos que mais otimizarão nossos estimadores, sem que seja necessário explorar todo o espaço de parâmetros (o que muitas vezes é impossível).

Explorando por mais tempo espaços maiores - Espaços maiores e sampling menores

Nós exploramos aleatoriamente o nosso espaço de parâmetros, mas fizemos isso de maneira bem restrita. Anteriormente, devido às limitações de processamento do GridSearchCV (principalmente em relação ao tempo), nós utilizamos somente 36 combinações.

Porém, seria mais interessante explorarmos ainda mais parâmetros no nosso algorítimo - por exemplo, um max_depth que recebesse 10, 20, 30 ou até que não tivesse limites (o que é possível com None, segundo a documentação do próprio GridSearchCV).

A ideia é executarmos novamente o RandomizedSearchCV, mas com diferentes customizações nesse espaço de parâmetros. Por exemplo, em max_depth, ao invés de termos somente os valores 3 e 5, teremos um conjunto discreto de números inteiros (3, 5, 10, 15, 20, 30) com a adição do valor None.

Em min_samples_split e min_samples_leaf, queremos qualquer número inteiro aleatório entre 32 e 128. Para isso, precisaremos de uma função de aleatoriedade que devolva um número aleatório a cada execução - neste caso, randint (random integer). Essa função deve ser importada do pacote scipy,stats.

Segundo a documentação do SciPy randint, ele percorre desde o número mais baixo (low, no nosso código 32) até o número anterior ao mais alto (high - 1, ou seja, 127).

Isso significa que agora temos muito mais possibilidades de combinações: são 7 elementos para max_depth, 96 para min_samples_split e min_samples_leaf, e 2 para criterion - no total, 129.024 combinações diferentes de parâmetros.

Desse número, executaremos apenas 16, a mesma quantidade que estávamos executando anteriormente, mas com um espaço de parâmetros muito maior e mais complexo:

from scipy.stats import randint

SEED=301
np.random.seed(SEED)

espaco_de_parametros = {
    "max_depth" : [3, 5, 10, 15, 20, 30, None],
    "min_samples_split" : randint(32, 128),
    "min_samples_leaf" : randint(32, 128),
    "criterion" : ["gini", "entropy"]

}

busca = RandomizedSearchCV(DecisionTreeClassifier(),
                    espaco_de_parametros, 
                    n_iter = 16,
                    cv = KFold(n_splits = 5, shuffle=True),
                          random_state = SEED)


busca.fit(x_azar, y_azar)
resultados = pd.DataFrame(busca.cv_results_)
resultados.head()

Em seguida, imprimiremos os resultados e o melhor conjunto na tela:

scores = cross_val_score(busca, x_azar, y_azar, cv = KFold(n_splits=5, shuffle=True))
imprime_score(scores)
melhor = busca.best_estimator_
print(melhor)

Como resposta, teremos algo como:

Accuracy médio 78.71

Intervalo [77.49, 79.93]

DecisionTreeClassifier(class_weight=None, criterion='entropy', max_depth=3,

        max_features=None, max_leaf_nodes=None,

        min_impurity_decrease=0.0, min_impurity_split=None,

        min_samples_leaf=71, min_samples_split=100,

        min_weight_fraction_leaf=0.0, presort=False, random_state=None,

        splitter='best')

Nossa acurácia foi bem próxima dos resultados anteriores, mas o ponto é que demoramos um tempo 8.000 vezes menor para explorar esse espaço de parâmetros, obtendo resultados tão bons quanto conseguiríamos com o GridSearchCV.

Sobre o curso Machine Learning parte 2: otimização com exploração aleatória

O curso Machine Learning parte 2: otimização com exploração aleatória possui 69 minutos de vídeos, em um total de 29 atividades. Gostou? Conheça nossos outros cursos de Machine Learning em Data Science, ou leia nossos artigos de Data Science.

Matricule-se e comece a estudar com a gente hoje! Conheça outros tópicos abordados durante o curso:

• Randomized Search e Cross validation combinadas
• Explorando por mais tempo espaços maiores
• Baseline com busca exaustiva no espaço discretizado
• Comparando com busca aleatória
• Otimização de hiper parâmetros sem validação cruzada (treino, teste e validação)