Otimização: encontrando soluções inteiras em programação linear

Problema e modelagem - Apresentação

Olá! Boas-vindas ao curso de Otimização: Programação Inteira e Programação Linear Inteira!

Já imaginou fazer aquela viagem dos sonhos, mas se vê perdido diante de tantas opções e não sabe por onde começar para economizar ao máximo e ainda aproveitar os pontos turísticos? Então este curso é para você! Meu nome é João Miranda e serei seu instrutor nesta jornada!

Audiodescrição: João se descreve como um homem branco, de cabelo médio preso em um coque, com as laterais raspadas, barba preta, e olhos pretos. Veste uma camisa preta lisa e está sentado em uma cadeira gamer nas cores preto e branco. Ao fundo, uma parede clara iluminada em degradê de verde e azul. Na parede, a gravura da Árvore de Gondor com a Espada do Rei ao centro, uma referência à saga "O Senhor dos Anéis".

Durante este curso, vamos desenvolver um projeto de otimização linear focado em soluções de valores inteiros, explorando um caso prático de planejamento de viagem para Paris. Nosso objetivo é encontrar o melhor cenário possível, levando em conta tanto os gastos quanto o tempo necessário para visitar as atrações turísticas.

Vamos entender o ramo da pesquisa operacional e suas principais ferramentas para tomar as melhores decisões considerando um conjunto de restrições. É importante destacar que não abordaremos otimizações não lineares, nossa ênfase será na programação linear inteira.

Para acompanhar o conteúdo, é importante que você tenha conhecimentos básicos de programação em Python e uma compreensão introdutória de pesquisa operacional. Vamos nessa?

Problema e modelagem - O problema de otimização

Para planejar uma viagem memorável a Paris, precisamos superar dois grandes desafios: um orçamento limitado e um tempo restrito para explorar a cidade, repleta de maravilhas. Como podemos maximizar essa experiência, selecionando as atrações ideais dentro dessas limitações? Como podemos garantir que visitaremos uma quantidade mínima de pontos turísticos nesse tempo limitado, equilibrando também o orçamento para uma experiência satisfatória?

Para abordar esses desafios, vamos utilizar o Google Colab e a linguagem Python para explorar as características das atrações turísticas, visualizá-las em um mapa e comparar suas informações. Em seguida, aplicaremos esses dados em um modelo de otimização linear para encontrar o cenário ideal considerando todas essas restrições.

Para começar, abriremos o Google Colab e acessaremos o notebook disponível na atividade "Preparando Ambiente". Se você deseja acompanhar os códigos conosco, basta baixar este notebook na atividade correspondente.

Passo 1 - armazenando o nome das atrações

O primeiro passo é armazenar as informações das atrações turísticas em nosso ambiente Python. Vamos começar copiando o código atracoes = [], que é uma lista com o nome de cada atração entre aspas duplas, como "Torre Eiffel", "Museu do Louvre", "Catedral de Notre-Dame", e assim por diante.

Vamos colar esse código na primeira célula do nosso notebook e executá-lo pressionando "Shift + Enter". Dessa forma, teremos armazenado os nomes de todas as atrações turísticas que desejamos visitar em nossa viagem.

atracoes = [
    "Torre Eiffel",
    "Museu do Louvre",
    "Catedral de Notre-Dame",
    "Sacré-Cœur",
    "Arco do Triunfo",
    "Jardim de Luxemburgo",
    "Sainte-Chapelle",
    "Place de la Concorde",
    "Panthéon",
    "Museu d'Orsay",
    "Stade de France",
    "Parc des Princes",
]

Passo 2 - armazenando as coordenadas geográficas

Para visualizarmos as atrações turísticas em um mapa, precisamos das coordenadas geográficas de cada uma delas. Vamos criar um dicionário contendo a posição geográfica de cada atração. Esse dicionário terá o nome da atração como chave e uma tupla para cada atração contendo sua latitude e longitude. Por exemplo, para a Torre Eiffel, teremos a tupla 48.85837, 2.29448. Vamos copiar e colar esse código na célula seguinte e executá-lo pressionando "Shift + Enter".

localizacao_atracoes = {
    "Torre Eiffel": (48.85837, 2.29448),
    "Museu do Louvre": (48.86115, 2.33929),
    "Catedral de Notre-Dame": (48.85329, 2.34449),
    "Sacré-Cœur": (48.88722, 2.3225),
    "Arco do Triunfo": (48.86889, 2.29448),
    "Jardim de Luxemburgo": (48.85661, 2.35222),
    "Sainte-Chapelle": (48.85329, 2.34449),
    "Place de la Concorde": (48.86667, 2.33333),
    "Panthéon": (48.85333, 2.34667),
    "Museu d'Orsay": (48.86667, 2.33333),
    "Stade de France": (48.83418, 2.33595),
    "Parc des Princes": (48.82761, 2.29809),
}

Passo 3 - armazenando o custo de entrada

Agora que temos o nome das atrações e suas coordenadas geográficas, vamos explorar outras características. Para nossa viagem, estabeleceremos um tempo máximo de 8 horas e um orçamento de 100 euros. Cada atração terá um custo de entrada e um tempo recomendado de visita. Essas informações serão essenciais para determinarmos o melhor roteiro. Elas serão utilizadas na modelagem do nosso problema de otimização linear.

A primeira informação será o custo de entrada das atrações. Vamos criar um dicionário onde as chaves serão os nomes das atrações e os valores serão os custos de entrada, por exemplo: 25 euros para a Torre Eiffel, 17 euros para o Museu do Louvre, e assim por diante. Vamos copiar e colar esse código na célula seguinte e executá-lo.

custo_entrada_atracoes = {
    "Torre Eiffel": 25,
    "Museu do Louvre": 17,
    "Catedral de Notre-Dame": 0,
    "Sacré-Cœur": 0,
    "Arco do Triunfo": 0,
    "Jardim de Luxemburgo": 0,
    "Sainte-Chapelle": 12,
    "Place de la Concorde": 0,
    "Panthéon": 8,
    "Museu d'Orsay": 17,
    "Stade de France": 15,
    "Parc des Princes": 12,
}

Passo 4 - armazenando o tempo recomendado de visita

Em seguida, criaremos outro dicionário com o tempo recomendado de visita em horas para cada atração. O processo será o mesmo: as chaves serão os nomes das atrações e os valores serão os tempos recomendados de visita. Por exemplo, 3 horas para a Torre Eiffel, 5 horas para o Museu do Louvre, e assim por diante. Vamos copiar e colar esse código na célula seguinte e executá-lo.

tempo_recomendado_atracoes = {
    "Torre Eiffel": 3,
    "Museu do Louvre": 5,
    "Catedral de Notre-Dame": 2,
    "Sacré-Cœur": 1,
    "Arco do Triunfo": 1,
    "Jardim de Luxemburgo": 3,
    "Sainte-Chapelle": 2,
    "Place de la Concorde": 3,
    "Panthéon": 1,
    "Museu d'Orsay": 2,
    "Stade de France": 2,
    "Parc des Princes": 2,
}

Passo 5 - construindo o mapa

Com todas essas informações, será difícil compará-las apenas visualizando o dicionário. Portanto, utilizaremos um mapa interativo, onde colocaremos marcadores para cada atração. Ao clicarmos em um marcador, será exibida a informação do tempo recomendado e do custo de entrada da atração.

Para construir o mapa, vamos utilizar uma biblioteca Python chamada Folium. Primeiro, vamos importar a biblioteca com o comando import folium. Em seguida, criaremos a camada de visualização do mapa centrada na cidade de Paris. Para isso, criaremos uma variável chamada mapa e atribuiremos folium.Map(). Como parâmetro, passaremos location, que corresponde à localização central do mapa, representada pela média das coordenadas das atrações turísticas, utilizando a latitude e longitude [48.856614, 2.352222]. Além disso, definiremos o zoom inicial do mapa como 12 com zoom_start = 12.

import folium

mapa = folium.Map(location = [48.856614, 2.352222], zoom_start = 12)

Depois de criar o mapa, adicionaremos marcadores para cada atração turística. Faremos isso usando um loop for na lista de atrações. Para cada atração, criaremos um pop-up (uma espécie de janela) contendo informações como nome da atração, custo de entrada e tempo recomendado de visita. Para isso, utilizaremos popup = folium.Popup(), passando um HTML para formatar as informações das atrações de forma legível.

Para formatar o texto em HTML dentro do pop-up, usaremos uma f-string e três aspas para permitir texto em várias linhas. Na primeira linha, incluiremos o nome da atração entre chaves, formatando-o em negrito com a tag HTML <b>. Para indicar o término do texto em negrito, usaremos </b>. Em seguida, para quebrar uma linha, usaremos a tag <br>.

Na segunda linha, inseriremos o tempo recomendado, acessando o valor correspondente no dicionário tempo_recomendado_atracoes. Aqui, especificaremos se é uma ou várias horas. Após uma nova quebra de linha, indicaremos o custo de entrada em euros.

Depois do HTML, definiremos o tamanho máximo do pop-up com max_width = 200, garantindo que o texto seja exibido adequadamente. Por fim, o parâmetro sticky = True permitirá a abertura de vários pop-ups ao mesmo tempo, facilitando a comparação de informações.

import folium

mapa = folium.Map(location = [48.856614, 2.352222], zoom_start = 12)
for atracao in atracoes:
    popup = folium.Popup(f'''<b>{atracao}</b><br>
    Tempo recomendado: {tempo_recomendado_atracoes[atracao]} hora(s)<br>
    Valor da entrada: € {custo_entrada_atracoes[atracao]}
    ''',
    max_width = 200,
    sticky = True)

Em seguida, adicionaremos um marcador para cada atração com folium.Marker(), passando a localização da atração e o pop-up correspondente. Depois, adicionaremos cada marcador ao mapa com .add_to(mapa). Por fim, chamaremos mapa para poder visualizá-lo.

import folium

mapa = folium.Map(location = [48.856614, 2.352222], zoom_start = 12)

for atracao in atracoes:
    popup = folium.Popup(f'''<b>{atracao}</b><br>
    Tempo recomendado: {tempo_recomendado_atracoes[atracao]} hora(s)<br>
    Valor da entrada: € {custo_entrada_atracoes[atracao]}
    ''',
    max_width = 200,
    sticky = True)
    folium.Marker(localizacao_atracoes[atracao], popup = popup).add_to(mapa)

mapa

Analisando o mapa

Ao executar este código com "Shift + Enter", poderemos visualizar o mapa.

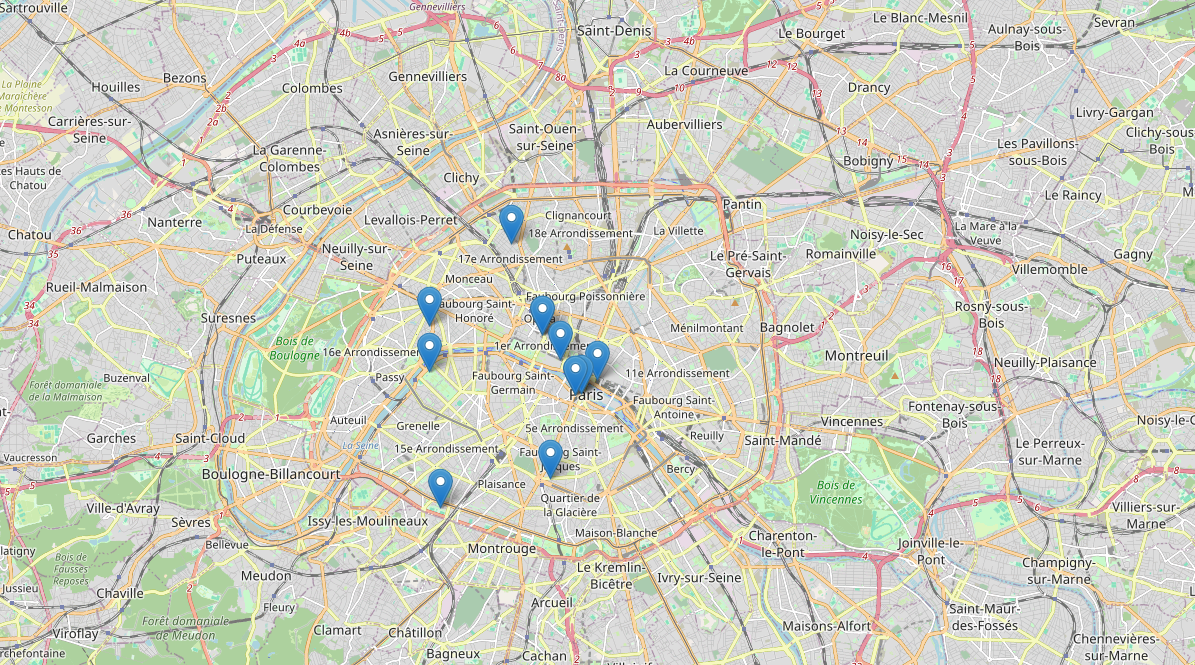
Note como é interessante observar a representação da cidade de Paris com vários marcadores em azul. Ao clicar em cada um desses marcadores, vemos o nome da atração turística em negrito, juntamente com o tempo recomendado de visita e o valor de entrada. Por exemplo, o Sacré-Cœur tem um tempo recomendado de 1 hora e entrada gratuita.

Ao clicar em outro marcador, como o Stade de France, veremos que o tempo recomendado é de 2 horas, com um custo de entrada de 15 euros. Então, podemos comparar diferentes atrações ao abrir os marcadores e explorar as informações de forma interativa. Além disso, é possível visualizar a distância entre cada uma das atrações para determinar se haverá um tempo considerável de deslocamento entre elas.

No entanto, mesmo com essa análise, ainda estamos realizando o processo manualmente. Será que existe uma maneira de automatizar a seleção das atrações turísticas para encontrar o melhor cenário possível? Vamos descobrir isso no próximo vídeo.

Problema e modelagem - Modelagem em programação linear

Com o intuito de planejar a viagem ideal para Paris, já reunimos as principais informações sobre as atrações turísticas e elaboramos um mapa para comparar esses dados. No entanto, apesar de auxiliar na análise, ainda há muitas possibilidades a considerar, e o mapa por si só não oferece uma resposta imediata. Será que existe um método para encontrar automaticamente o melhor itinerário?

Podemos empregar algoritmos de programação linear para determinar o cenário ideal, levando em conta todas as restrições, como o tempo máximo disponível e o orçamento estipulado para a viagem. Para isso, é necessário traduzir nosso problema em um modelo matemático. Este modelo será crucial para representar cada restrição, variável e para definir uma função objetivo a ser maximizada ou minimizada. Em nosso caso, a função objetivo será minimizar os custos da viagem. A construção deste modelo matemático é essencial para resolver problemas de programação linear.

Traduzindo o problema em um modelo matemático

Antes de avançar para a implementação do código, é fundamental garantir que o modelo matemático esteja bem estruturado e compreensível, para que a solução obtida seja a desejada. O primeiro passo é criar um conjunto de dados para indexar nosso problema.

No Google Colab, temos um texto detalhado com todas as informações sobre o modelo matemático a ser desenvolvido.

Texto omitido. Para acessá-lo, consulte o notebook disponibilizado.

Conjuntos

Inicialmente, vamos construir o conjunto de características para indexar nosso problema. Todas as variáveis e restrições dependerão dessa indexação, que, no caso, corresponde aos pontos turísticos. As informações, como tempo recomendado de visita e custo de entrada, estão relacionadas aos pontos turísticos. Portanto, para realizar essa indexação, vamos criar um conjunto de pontos turísticos em nosso modelo matemático.

O parâmetro utilizado aqui será pontos_turisticos.

Parâmetros

Após essa etapa, vamos estabelecer os parâmetros. Esses parâmetros serão valores fixos essenciais para o nosso problema. Com base nesses valores fixos, poderemos estabelecer restrições e utilizá-los na função objetivo. Existem parâmetros que não dependem das atrações turísticas, ou seja, são independentes, como o tempo máximo disponível. Definiremos que o tempo máximo para a viagem será de 8 horas. Além disso, estabeleceremos um número mínimo de atrações que desejamos visitar. Esse número será fixo, e nosso modelo usará esse valor para encontrar a solução.

Após esses dois parâmetros, o tempo recomendado para visita de cada ponto turístico também será estabelecido. Por isso, na variável que está sendo construída, tempo_recomendado, incluímos o índice ponto. Esse tempo recomendado dependerá de cada ponto turístico, mas também será um valor fixo. Ao fixarmos esse valor para cada atração, o modelo o considerará durante a execução.

Por último, precisaremos determinar o custo de entrada, que também é específico para cada ponto turístico. Daí a necessidade da indexação dos conjuntos. Com base nessa indexação, o modelo poderá identificar o tempo recomendado e o custo de entrada para cada atração.

Os parâmetros desta etapa são: tempo_maximo, num_min_atracoes, tempo_recomendado [ponto] e custo_entrada [ponto].

Variáveis de decisão

Após definirmos os parâmetros do nosso modelo matemático, vamos estabelecer as variáveis de decisão. Essas variáveis, como sugere o nome, variam durante a execução do modelo. Essas variáveis de decisão serão as que representam as visitas a cada ponto turístico. Novamente, essas variáveis de decisão estarão indexadas para cada ponto turístico, mas seus valores variam e dependem da solução do problema. É justamente esses valores que desejamos determinar para decidir se visitaremos ou não um determinado ponto turístico.

Para determinar se um ponto turístico será visitado ou não, podemos usar o valor da variável de visita. Se essa variável for 0, indica que o ponto turístico não será visitado. Por outro lado, se for 1, significa que o ponto será visitado. Portanto, essa variável pode variar entre 0 e 1, e o modelo decidirá com base nas restrições estabelecidas.

A variável utilizada aqui será visitas[ponto].

Função objetivo

Após a definição dessas variáveis de decisão, precisamos de uma função objetivo para nosso modelo matemático. Essa função objetivo é fundamental para determinar o melhor cenário possível. No nosso caso, buscamos minimizar os custos da viagem. Como podemos expressar essa função objetivo para minimizar os custos? Podemos usar os parâmetros de custo de entrada de cada atração. Para calcular o custo total da viagem, somamos os custos de entrada de todas as atrações que visitamos.

Por isso, precisamos da variável de decisão para saber se cada ponto será visitado ou não. Se decidirmos visitar um ponto, a variável correspondente será igual a 1, e o custo de entrada dessa atração será multiplicado por 1. Se decidirmos não visitar um ponto, a variável será 0, e o custo de entrada dessa atração será multiplicado por 0, resultando em 0 custo.

Somando todas essas multiplicações, obteremos o custo total da viagem. Para minimizar esse custo, utilizaremos a função de minimizar para encontrar o menor valor possível da função objetivo. O modelo ajustará os valores das variáveis de decisão para determinar a combinação que minimize os custos da viagem.

Restrições

Depois de definir a função objetivo, nosso modelo precisará de restrições, que são as limitações ou condições que queremos impor para encontrar o melhor cenário possível. A primeira delas é o número mínimo de visitas. Não adianta minimizar os custos da viagem se não visitarmos nenhuma atração. Portanto, precisamos estabelecer um número mínimo de atrações a visitar e criar uma restrição que exija que o número total de visitas seja igual ou superior a esse valor mínimo.

Para calcular o número de visitas na viagem, podemos simplesmente somar as variáveis de decisão de visitação. Se uma variável for igual a 1, significa que a atração correspondente foi visitada. Portanto, somando todos os valores iguais a 1, obtemos a quantidade total de atrações visitadas. Devemos impor uma restrição de que essa soma seja maior ou igual ao número mínimo de visitas desejado.

Além disso, precisamos impor uma restrição de tempo. Cada atração possui um tempo recomendado de visita, e temos um limite de tempo de 8 horas para a viagem. Portanto, precisamos garantir que a soma dos tempos de visita das atrações visitadas não ultrapasse as 8 horas. Para isso, multiplicamos o tempo recomendado de cada atração pela variável de decisão correspondente. Se a atração for visitada (variável igual a 1), o tempo recomendado será mantido; caso contrário, será zero. Somando todos esses tempos de visita, obtemos a duração total da viagem, que deve ser menor ou igual a 8 horas.

Com todas essas restrições modeladas em expressões matemáticas, estamos prontos para transformá-las em código de programação para resolver o problema. É o que abordaremos no próximo vídeo!

Sobre o curso Otimização: encontrando soluções inteiras em programação linear

O curso Otimização: encontrando soluções inteiras em programação linear possui 156 minutos de vídeos, em um total de 46 atividades. Gostou? Conheça nossos outros cursos de Data Science em Data Science, ou leia nossos artigos de Data Science.

Matricule-se e comece a estudar com a gente hoje! Conheça outros tópicos abordados durante o curso:

• Problema e modelagem
• Encontrando soluções inteiras
• Refinando restrições
• Explorando variações no modelo de planejamento
• Desafios em modelagem com dados extensos