Boas-vindas! Me chamo Mirla Costa, sou instrutora aqui na Alura e irei te acompanhar neste curso.
Audiodescrição: Mirla se autodeclara como uma mulher de pele clara, de cabelos cacheados e pretos, abaixo da altura dos ombros. Usa óculos de grau de armação redonda. Ela veste uma camiseta preta lisa. Ao fundo, uma parede com uma iluminação azul e verde com duas estantes com decorações.
Você já pensou em prever o futuro, não através de adivinhação ou misticismo, mas usando modelos matemáticos e ciência de dados? Neste curso, aprenderemos a prever valores de temperatura aplicando modelos matemáticos em séries temporais.
O projeto tem como objetivo permitir a previsão de temperaturas para os anos de 2025, 2026 e até 2027, utilizando modelos matemáticos aplicados em séries temporais, a partir de dados disponíveis em 2024.
Durante o curso, serão utilizadas a linguagem Python e as bibliotecas Pandas e Matplotlib para a preparação dos dados. Para a criação e avaliação dos modelos, será utilizada a biblioteca StatsModel.
Para aproveitar ao máximo este curso, é recomendado já ter conhecimento em Python e nas bibliotecas Pandas e Matplotlib. Também é importante estar familiarizado com séries temporais e suas principais características.
Vamos lá?
Somos pessoas pesquisadoras de um instituto de meteorologia e frequentemente recebemos pedidos de empresas e serviços que precisam de informações climáticas para suas atividades. Recentemente, um empreendimento do setor agropecuário solicitou previsões de temperaturas mensais para os próximos três anos em três locais onde planejam abrir novas fazendas.
Essas informações são essenciais para o planejamento de plantio e colheita. Já temos os dados climáticos das áreas próximas e estamos prontos para começar o projeto.
Que tipo de dado estamos tratando? Como vamos prever essa informação?
Primeiro, precisamos coletar os dados que usaremos. Como temos três localidades para estudar, é importante organizar o projeto. Vamos começar pela fazenda 1, analisando uma localidade por vez.
Com o notebook aberto e conectado ao Google Colab.
Lembre-se: este notebook e os links para todos os dados estarão disponíveis nas atividades desta aula. Acesse, baixe o notebook e vamos trabalhar juntos neste projeto!
Célula no Google Colab:
dados_f1 = 'https://raw.githubusercontent.com/Mirlaa/s-ries-temporais-statsmodels/main/Dados/Temperatura_mensal_F1.csv'
dados_f2 = 'https://raw.githubusercontent.com/Mirlaa/s-ries-temporais-statsmodels/main/Dados/Temperatura_mensal_F2.csv'
dados_f3 = 'https://raw.githubusercontent.com/Mirlaa/s-ries-temporais-statsmodels/main/Dados/Temperatura_mensal_F3.csv'
Já temos o link para cada conjunto de dados: f1 para a fazenda 1, f2 para a fazenda 2 e f3 para a fazenda 3. Executamos essa célula clicando no ícone de play à esquerda ou teclando "Shift + Enter" para salvar esses links nas variáveis correspondentes.
Para o nosso projeto, precisamos importar as bibliotecas básicas para tratamento e manipulação de dados em ciência de dados. Usaremos o Pandas e o Matplotlib. Na célula seguinte, digitamos import pandas as pd, teclamos "Enter" para pular uma linha, e digitamos import matplotlib.pyplot as plt.
import pandas as pd
import matplotlib.pyplot as plt
Pressionamos "Shift + Enter" para executar a célula.
Coletamos os dados e os armazenamos em um dataframe chamado df_f1. Para isso, utilizamos o comando pd.read_csv() para ler o arquivo dados_f1.
Digitamos df_f1 = pd.read_csv(dados_f1), pressionamos "Enter" para pular linha, e depois digitamos df_f1 e pressionamos "Shift + Enter" para visualizar o dataframe.
df_f1 = pd.read_csv(dados_f1)
df_f1
Obtemos como retorno:
| # | DATA | TEMP |
|---|---|---|
| 0 | 1963-05-01 | 23.11 |
| 1 | 1963-06-01 | 24.20 |
| 2 | 1963-07-01 | 25.37 |
| 3 | 1963-08-01 | 23.86 |
| 4 | 1963-09-01 | 23.03 |
| ... | ... | ... |
| 727 | 2023-12-01 | 19.49 |
| 728 | 2024-01-01 | 19.28 |
| 729 | 2024-02-01 | 19.73 |
| 730 | 2024-03-01 | 20.44 |
| 731 | 2024-04-01 | 22.07 |
O dataframe contém duas colunas de dados: uma com informações sobre a data e outra com informações sobre a temperatura. A coluna de data mostra os meses, começando em maio de 1963 e seguindo até abril de 2024. Isso significa que temos dados mensais de temperatura, formando uma série temporal.
Cada mês tem uma temperatura registrada, e esses dados representam a temperatura de uma localidade próxima à Fazenda 1.
Vamos ajustar os dados para facilitar a visualização das informações. Primeiro, transformamos a coluna de DATA no tipo datetime. Para isso, usamos o comando df_f1['DATA'] = pd.to_datetime(df_f1['DATA'], format='%Y-%m-%d'), sendo o %d para o dia, o %m para o mês e o %Y para o ano.
Em seguida, podemos definir a coluna de DATA como o index do dataframe, o que destaca a série temporal. Para isso, usamos df_f1.set_index(['DATA'], inplace=True, drop=True). Finalmente, para visualizar os dados ajustados, digitamos df_f1.
df_f1['DATA'] = pd.to_datetime(df_f1['DATA'], format='%Y-%m-%d')
df_f1.set_index(['DATA'], inplace=True, drop=True)
df_f1
Pressionamos "Shift + Enter" para rodar a célula. Com o conjunto de dados organizado, vamos plotá-lo usando df_f1.plot(figsize=(12,6)).
df_f1.plot(figsize=(12,6))
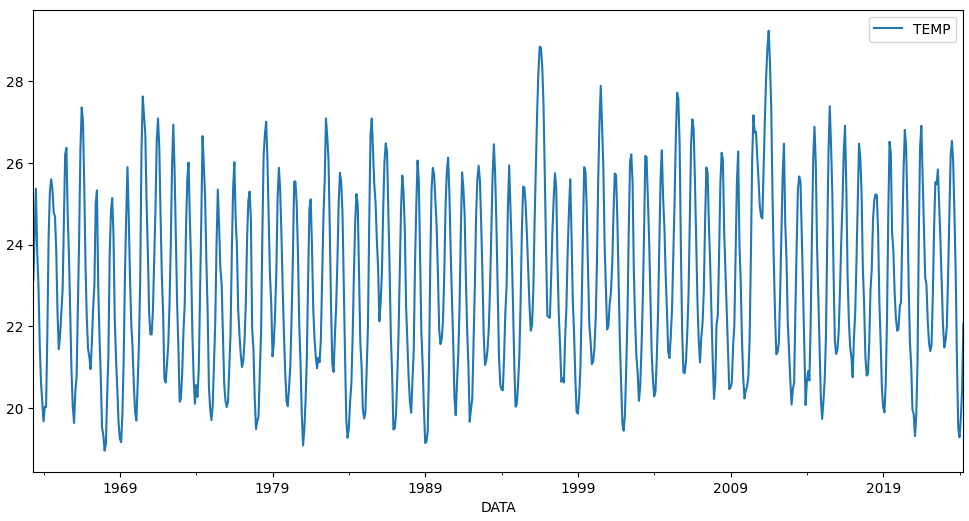
Observamos uma série temporal típica de dados de temperatura, com meses mais frios e meses mais quentes. Essa visualização destaca claramente as variações sazonais, mostrando como as temperaturas mudam ao longo do tempo, o que é característico de dados climáticos.
Para prever os dados, utilizamos um modelo simples chamado modelo naive ("ingênuo"), que atribui o valor do mês passado ao próximo mês. Aplicamos esse modelo usando df_f1.shift(1), sendo shift() um método que consegue passar os dados para frente e no caso, definimos como 1.
df_f1.shift(1)
Obtemos como retorno:
| DATA | TEMP |
|---|---|
| 1963-05-01 | NaN |
| 1963-06-01 | 23.11 |
| 1963-07-01 | 24.20 |
| 1963-08-01 | 25.37 |
| 1963-09-01 | 23.86 |
| ... | ... |
| 2023-12-01 | 21.11 |
| 2024-01-01 | 19.49 |
| 2024-02-01 | 19.28 |
| 2024-03-01 | 19.73 |
| 2024-04-01 | 20.44 |
Com isso, o valor de temperatura de maio é atribuído a junho (23.11), o valor de junho a julho, e assim por diante. No entanto, esse método apresenta uma limitação.
Para prever os valores mensais por três anos, simplesmente repetir o valor anterior não é suficiente, pois resultaria em uma linha reta constante, o que não atende às nossas necessidades para uma previsão mais precisa.
Algo que resolve o nosso problema é utilizar modelos matemáticos que captam padrão nos dados e conseguem gerar uma série correspondente aos valores passados, não só repetindo os dados. Checaremos qual modelo matemático funciona para os nossos dados no próximo vídeo!
Coletamos os dados e aplicamos um modelo ingênuo. Contudo, essa abordagem mostrou-se pouco eficaz, pois o modelo ingênuo não consegue capturar padrões em séries temporais e, portanto, não consegue aplicar o que aprendeu para prever valores futuros. Ele apenas reproduz os valores anteriores.
Por outro lado, modelos matemáticos são capazes de captar esses padrões e fornecer previsões mais precisas. É necessário identificar qual modelo matemático se ajusta melhor aos dados e consegue identificar esses padrões de forma eficaz.
Para determinar o modelo ideal a ser aplicado, é necessário realizar uma análise detalhada da série temporal, identificando características essenciais que ela deve ter. Um aspecto fundamental a ser examinado é a estacionaridade.
Uma série temporal é considerada estacionária quando sua média e variância permanecem constantes ao longo do tempo, o que indica que não é afetada por tendências ou componentes sazonais. Nesse caso, os valores futuros dependem dos valores passados. Portanto, podemos aplicar um modelo que compreende essas relações passadas para fazer previsões sobre o futuro.
Para avaliar a estacionaridade da série temporal, podemos aplicar dois testes: o ADF e o KPSS. Ambos os testes verificam a presença de uma raiz unitária, que indica se a série é não estacionária. Com base nos resultados desses testes, podemos determinar se a série é ou não estacionária.
Para mais informações sobre estacionaridade, a raiz unitária e os detalhes desses testes, consulte as atividades desta aula, que oferecem um aprofundamento sobre esses pontos.
Vamos agora usar o Google Colab para construir as funções que aplicarão os testes na nossa série temporal.
A biblioteca StatsModels, disponível no Google Colab, fornece funções, métodos e modelos matemáticos para trabalhar com séries temporais. Para aplicar os testes ADF e KPSS, utilizaremos as funções oferecidas por essa biblioteca.
Na próxima célula disponível do notebook, importamos as funções necessárias. Para isso, digitamos from statsmodels.tsa.stattools
e, em seguida, importamos o teste ADF e o teste KPSS usando import adfuller, kpss.
Por enquanto, temos:
from statsmodels.tsa.stattools import adfuller, kpss
Como ainda vamos trabalhar com outras séries temporais e realizar análises adicionais em nosso projeto, vamos criar uma função def para aplicar esses testes a diferentes conjuntos de dados.
Criamos uma função def chamada estac(), que aceitará df como parâmetro, a variável contendo o DataFrame Temporal. Na mesma célula, criamos a variável adf, que será igual a adfuller() com os parênteses apropriados. Dentro dessa função, passamos a variável df.
from statsmodels.tsa.stattools import adfuller, kpss
def estac(df):
adf = adfuller(df)
Essa função do StatsModels realizará todos os estudos estatísticos necessários e coletará os dados. Nossa tarefa será apenas verificar os resultados, sem precisar nos preocupar com os detalhes dos parâmetros matemáticos.
Deixamos um código pronto para agilizar nosso vídeo:
from statsmodels.tsa.stattools import adfuller, kpss
def estac(df):
adf = adfuller(df)
print(f'Valor-p do Teste ADF: {adf[1]:.4f}')
if adf[1] > 0.05:
print('Não rejeitar a Hipótese Nula: a série não é estacionária\n')
else:
print('Rejeitar a Hipótese Nula: a série é estacionária\n')
A instrutora não executa a célula ainda.
Usamos "Ctrl + F" para conferir o que foi incluído. O código contém um comando print() para exibir o Valor-p do teste ADF.
O comando print está configurado da seguinte forma: print(f'Valor-p do Teste ADF: {adf[1]:.4f}'). Utilizamos [1] para acessar o Valor-p, que é o segundo valor retornado pelo teste, e escolhemos exibir apenas o valor 4f para evitar que o resultado fique muito extenso.
No teste ADF, a hipótese nula assume a presença de uma raiz unitária, ou seja, considera que a série é não estacionária.
Se o Valor-p do teste, acessado por adf[1], for maior que 0,05 (considerando um intervalo de confiança de 95%), exibimos uma mensagem com print(), indicando que não rejeitamos a hipótese nula e, portanto, a série é não estacionária.
Adicionamos um \n para separar essa mensagem de um outro teste que será incluído em seguida. Por outro lado, no else, se o Valor-p for menor ou igual a 0,05, rejeitamos a hipótese nula, concluindo que a série é estacionária.
Agora, passamos para o segundo teste, o KPSS. Criamos uma variável chamada kpss_saida, que será igual a kpss(df). Colamos o código com "Ctrl + V", e observamos que é bem semelhante ao código do adf.
from statsmodels.tsa.stattools import adfuller, kpss
def estac(df):
adf = adfuller(df)
print(f'Valor-p do Teste ADF: {adf[1]:.4f}')
if adf[1] > 0.05:
print('Não rejeitar a Hipótese Nula: a série não é estacionária\n')
else:
print('Rejeitar a Hipótese Nula: a série é estacionária\n')
kpss_saida = kpss(df)
print(f'Valor-p do Teste KPSS: {kpss_saida[1]:.4f}')
if kpss_saida[1] > 0.05:
print('Não rejeitar a Hipótese Nula: a série é estacionária\n')
else:
print('Rejeitar a Hipótese Nula: a série não é estacionária\n')
Executamos a célula.
A principal diferença é que, em vez de exibir o valor-p do adf, exibimos o valor-p do kpss. O kpss possui uma estrutura de saída semelhante à do adf, mas sua hipótese nula é que não há raiz unitária, ou seja, a série é estacionária.
Se o valor-p for superior a 0,05, não rejeitamos a hipótese nula, o que indica que a série é estacionária. Caso o valor-p seja inferior a 0,05, rejeitamos a hipótese nula e concluímos que a série é não estacionária.
Aplicaremos a nossa função com estac(df_f1).
estac(df_f1)
Obtemos:
Valor-p do Teste ADF: 0.0000
Rejeitar a Hipótese Nula: a série é estacionária
Valor-p do Teste KPSS: 0.0798
Não rejeitar a Hipótese Nula: a série é estacionária
A saída mostrará que a série é estacionária. Com a confirmação de que a série é estacionária, podemos utilizar um modelo autoregressivo para prever os valores futuros desse conjunto de dados.
Antes de abordarmos e criarmos o modelo, precisamos dividir os dados em um conjunto de treino e outro de teste para avaliarmos o modelo posteriormente. Para fazer essa divisão, criaremos uma variável chamada divisao, que determinará o index exato onde a separação entre os conjuntos de treino e teste ocorrerá.
Para o tamanho dos nossos dados, podemos dividir 70% dos dados para treino e os 30% restantes para teste.
Digitamos int(), que será calculada como len(df_f1)*0.70, correspondendo a 70% dos dados. Em seguida, criaremos a variável de treino. Para isso, faremos a divisão dentro do conjunto total de dados usando df_f1.iloc[:divisao] para selecionar todos os dados até o ponto de divisão.
Por fim, definimos a frequência dos dados para que o modelo possa entendê-la. Usaremos o método asfreq(''), definindo a frequência como MS para indicar que os dados são mensais.
Por enquanto, temos:
divisao = int(len(df_f1)*0.70)
treino = df_f1.iloc[:divisao].asfreq('MS')
Para o conjunto de teste, aplicamos um procedimento semelhante:
divisao = int(len(df_f1)*0.70)
treino = df_f1.iloc[:divisao].asfreq('MS')
teste = df_f1.iloc[divisao:].asfreq("MS")
Definimos a variável teste como df_f1.iloc[divisao:], começando a partir do ponto de divisão para fora (divisao:). Em seguida, definimos a frequência como MS para indicar que os dados são mensais.
Teclamos "Shift + Enter". Com isso, conseguimos dividir os nossos dados em conjuntos de treino e teste.
Agora que verificamos a estacionalidade, decidimos o modelo a ser utilizado e dividimos o conjunto de dados, vamos abordar e construir o modelo autoregressivo no próximo vídeo!
O curso Regressão: realizando previsão de séries temporais com statsmodels possui 128 minutos de vídeos, em um total de 54 atividades. Gostou? Conheça nossos outros cursos de Machine Learning em Data Science, ou leia nossos artigos de Data Science.
Matricule-se e comece a estudar com a gente hoje! Conheça outros tópicos abordados durante o curso:
Impulsione a sua carreira com os melhores cursos e faça parte da maior comunidade tech.
2 anos de Alura
Matricule-se no plano PLUS 24 e garanta:
Jornada de estudos progressiva que te guia desde os fundamentos até a atuação prática. Você acompanha sua evolução, entende os próximos passos e se aprofunda nos conteúdos com quem é referência no mercado.
Mobile, Programação, Front-end, DevOps, UX & Design, Marketing Digital, Data Science, Inovação & Gestão, Inteligência Artificial
Formações com mais de 1500 cursos atualizados e novos lançamentos semanais, em Programação, Inteligência Artificial, Front-end, UX & Design, Data Science, Mobile, DevOps e Inovação & Gestão.
A cada curso ou formação concluído, um novo certificado para turbinar seu currículo e LinkedIn.
No Discord, você participa de eventos exclusivos, pode tirar dúvidas em estudos colaborativos e ainda conta com mentorias em grupo com especialistas de diversas áreas.
Faça parte da maior comunidade Dev do país e crie conexões com mais de 120 mil pessoas no Discord.
Acesso ilimitado ao catálogo de Imersões da Alura para praticar conhecimentos em diferentes áreas.
Explore um universo de possibilidades na palma da sua mão. Baixe as aulas para assistir offline, onde e quando quiser.
Acelere o seu aprendizado com a IA da Alura e prepare-se para o mercado internacional.
2 anos de Alura
Todos os benefícios do PLUS 24 e mais vantagens exclusivas:
Luri é nossa inteligência artificial que tira dúvidas, dá exemplos práticos, corrige exercícios e ajuda a mergulhar ainda mais durante as aulas. Você pode conversar com a Luri até 100 mensagens por semana.
Aprenda um novo idioma e expanda seus horizontes profissionais. Cursos de Inglês, Espanhol e Inglês para Devs, 100% focado em tecnologia.
Para estudantes ultra comprometidos atingirem seu objetivo mais rápido.
2 anos de Alura
Todos os benefícios do PRO 24 e mais vantagens exclusivas:
Mensagens ilimitadas para estudar com a Luri, a IA da Alura, disponível 24hs para tirar suas dúvidas, dar exemplos práticos, corrigir exercícios e impulsionar seus estudos.
Envie imagens para a Luri e ela te ajuda a solucionar problemas, identificar erros, esclarecer gráficos, analisar design e muito mais.
Escolha os ebooks da Casa do Código, a editora da Alura, que apoiarão a sua jornada de aprendizado para sempre.
Conecte-se ao mercado com mentoria individual personalizada, vagas exclusivas e networking estratégico que impulsionam sua carreira tech para o próximo nível.